
Encryption-Friendly LLM Architecture (ICLR 2025)
Donghwan Rho*, Taeseong Kim*, Minje Park, Jung Woo Kim, Hyunsik Chae, Ernest K. Ryu† , Jung Hee Cheon†
ABSTRACT
- 문제 제기: 사용자 상호작용을 기반으로 개인 맞춤 응답을 제공하는 LLM 서비스는 편리하지만, 이 과정에서 사용자의 민감한 데이터가 노출될 수 있다는 심각한 프라이버시 문제를 야기합니다.
- 동형암호(HE) 소개: HE는 암호화된 상태에서 산술 연산을 수행할 수 있는 암호화 프로토콜로, 데이터 프라이버시를 보호하면서 머신러닝을 수행하는 프라이버시 보존 머신러닝(PPML) 분야의 잠재적 해결책으로 주목받고 있습니다. HE 외에도 PPML에는 Secure Multi-Party Computation (MPC) 이나 차분 프라이버시(Differential Privacy) 등의 기술이 있습니다.
- HE 적용의 어려움: LLM의 근간을 이루는 트랜스포머(Attention is All you Need)는 계산량이 매우 많으며, 행렬 곱셈 및 비다항식 연산(non-polynomial operations)에 크게 의존합니다. 이러한 연산을 암호화된 상태에서 직접 수행하면 엄청난 계산 시간과 정밀도 손실이 발생하여 HE를 LLM에 적용하는 것이 어렵습니다.
- 본 연구의 제안: 이 논문은 개인 맞춤 (사설) 파인튜닝 후의 추론(inference)에 중점을 둔, HE 친화적인 트랜스포머 아키텍처 수정 버전을 제안합니다.
- 주요 기술
- LoRA (Low-Rank Adaptation) 파인튜닝: 모델의 전체 가중치를 업데이트하는 대신, 일부 중요 레이어에 작은 저계수(low-rank) 행렬인 어댑터(adapter)를 추가하여 파인튜닝하는 방식입니다. 이 논문에서는 LoRA를 활용하여 HE 환경에서 발생하는 큰 규모의 암호문-암호문 행렬 곱셈(CCMM) 연산을 줄이는 데 사용했습니다.
- 가우시안 커널(Gaussian kernels, GK): 트랜스포머의 어텐션 메커니즘에서 사용되는 소프트맥스(softmax) 함수를 대체합니다. 소프트맥스는 HE 하에서 계산하기 매우 어려운 비다항식 함수인데, 가우시안 커널은 이를 더 간단하게 대체하여 계산 속도를 높입니다.
- 연구 성과
- 이러한 HE 친화적인 아키텍처 수정을 통해, 일반 모델과 유사한 성능을 유지하면서도 파인튜닝에서 6.94배, 추론에서 2.3배의 상당한 계산 속도 향상을 달성했습니다.
- 본 연구 결과는 데이터 보호가 중요한 분야에서 프라이버시를 보존하는 LLM 서비스를 제공할 수 있다는 가능성을 보여주는 실행 가능한 개념 증명(proof of concept)을 제공합니다.
- 이 연구는 기존의 HE 기반 PPML 연구들이 주로 암호화된 데이터에 대한 추론에 집중하고, 계산 복잡성 때문에 파인튜닝을 간과했던 한계를 넘어섰다는 점에서 중요합니다. LoRA를 활용하여 파인튜닝 과정까지 HE로 보호할 수 있음을 보였습니다. 또한, HE에 적용하기 어려운 소프트맥스 대신 가우시안 커널을 사용하는 등, HE 환경에 맞게 ML 모델 구조를 설계하는 방향을 제시하고 있습니다.
1 Introduction
- PPML(Privacy-Preserving Machine Learning)
- 사용자 데이터의 개인 정보 보호를 보장하면서 기계 학습을 수행하는 방법을 의미합니다.
- 이는 사용자와 상호 작용하며 개인화된 응답을 제공하는 LLM(Large Language Model)이 야기하는 심각한 개인 정보 보호 문제에 대한 해결책으로 등장했습니다.
- GDPR 및 CCPA 와 같은 규제가 강화되고, 심지어 특정 국가에서는 ChatGPT 사용이 일시적으로 금지되거나(McCallum, 2023) Apple, Samsung과 같은 기업에서 사내 사용을 제한하는(Mok, 2023) 등 개인 정보 보호의 중요성이 커지고 있습니다.
- 주요 PPML 기술
- MPC (Secure Multi-Party Computation)
- 차등 개인 정보 보호(Differential Privacy) : Inversion attacks 로 인한 보안성 이슈가 있습니다.
- 동형 암호화(HE, Homomorphic Encryption)
- MPC와 HE의 특징: PPML 의 세 가지 기술 중 MPC와 HE만이 암호학적 가정을 기반으로 증명 가능한 보안(provable security)을 제공합니다.
- MPC: 여러 당사자 간의 통신을 활용하여 계산을 수행합니다. 하지만 이는 신경망의 방대한 계산을 가속화하고 병렬화하는 데 어려움을 줄 수 있습니다.
- Homomorphic Encryption (HE)
- 통신 없이 암호화된 상태에서 산술 연산을 지원합니다. Fully homomorphic encryption using ideal lattices의 선구적인 작업 이후 다양한 HE 스킴이 개발되었습니다
- CKKS (Cheon et al., 2017) 스킴은 대규모 실수(real-valued) 데이터를 병렬로 평가하는 데 매우 효율적이며 PPML 연구에서 널리 사용됩니다
- HE를 LLM에 적용하는 도전 과제들
- 이론적으로 HE는 LLM 관련 개인 정보 보호 문제에 대한 효과적인 해결책을 제시하지만, HE 연산의 이론 및 구현에서 상당한 진전이 있었음에도 불구하고 LLM의 계산 규모 때문에 LLM을 HE로 보호하는 것은 여전히 어려운 문제입니다.
- Transformer 모델은 수많은 행렬 곱셈(matrix multiplications)과 다양한 비다항식 연산(non-polynomial operations)에 크게 의존합니다.
- 이러한 연산들을 HE에 직접 적용할 경우 상당한 계산 시간과 정확도 손실이 발생합니다. 본 논문은 이러한 문제점을 해결하기 위해 LoRA(Low-Rank Adaptation) 및 Gaussian Kernel을 활용하여 HE 친화적인 Transformer 아키텍처를 제안하고 있습니다.
- 연구의 주요 목표
- 이 논문은 대규모 언어 모델(LLM)에서 사용자 상호작용에 기반한 개인화된 응답이 사용자 프라이버시 문제를 야기하는 상황을 해결하고자 합니다. 기존의 동형 암호화(Homomorphic Encryption, HE) 기반 트랜스포머 모델 연구들이 복잡성 때문에 Fine-tuning 단계를 간과했던 문제에 주목하며, Fine-tuning 이후의 추론에 중점을 둔 새로운 HE 친화적 트랜스포머 아키텍처를 제안합니다.
- 이 아키텍처는 두 가지 주요 알고리즘 구성 요소를 활용하여 HE 환경에서 암호화된 트랜스포머 계산을 크게 가속화하고, 일반 텍스트 모델과 유사한 성능을 유지합니다.
- LoRA Fine-tuning 도입
- 목표: HE 환경에서 Fine-tuning 시 발생하는 주요 계산 병목인 대규모 암호문-암호문 행렬 곱셈(Ciphertext-Ciphertext Matrix Multiplications, CCMM)의 비용을 줄입니다.
- 효과: LoRA를 사용하면 업데이트되는 가중치의 수가 현저히 줄어들어, 많은 대규모 CCMM을 더 효율적인 평문-암호문 행렬 곱셈(Plaintext-Ciphertext Matrix Multiplications, PCMM) 및 더 작은 CCMM로 변환합니다. 이는 계산 속도 향상에 기여하며, Fine-tuning 시 필요한 파라미터 수가 줄어들어 AdamW 옵티마이저와 같은 비다항 함수(non-polynomial functions)의 계산 부담도 경감합니다.
- 어텐션(Attention) 레이어의 Softmax를 Gaussian Kernels (GK)로 대체
- 목표: HE는 다항식 연산만 지원하므로, Softmax와 같이 지수, 나눗셈, 최댓값 함수 등 비다항 연산이 포함된 함수는 HE 환경에서 구현하기 매우 어렵습니다.
- 효과: Gaussian Kernels는 이러한 비다항 연산을 회피할 수 있어, HE 환경에서 Softmax 함수를 평가하는 것보다 훨씬 효율적입니다. 특히, 나눗셈이나 최댓값 함수를 계산할 필요가 없으며, 지수 함수도 exp(x)를 x ≤ 0 범위에서만 근사하면 되므로 수치적으로 안정적입니다.
- 연구 결과
- CKKS 동형암호 스킴을 사용하여 암호화된 데이터로 수정된 BERT 모델을 실험한 결과, Fine-tuning에서 6.94배, 추론에서 2.3배의 상당한 계산 속도 향상을 달성했습니다.
- 이는 데이터 보호가 중요한 분야에서 프라이버시를 보호하는 LLM 서비스를 제공할 수 있는 실현 가능한 개념 증명을 제시합니다.
- 이 연구는 동형 암호화 분야의 중요한 진전을 보여주며, 특히 LoRA [1] 에서 제시된 파라미터 효율적인 Fine-tuning 방법론을 HE 환경에 성공적으로 적용했다는 점에서 의미가 있습니다. 또한 어텐션 메커니즘의 핵심 요소인 Softmax를 [2] 에서 사용된 방식과 달리 Gaussian Kernels (GK) 로 대체함으로써 HE 의 계산 제약을 우회하는 독창적인 접근 방식을 보여줍니다.
1.1 Prior Work
Transformer-based language models and LoRA
- 트랜스포머 기반 언어 모델의 유형
- 인코더 전용 모델 (Encoder-only models): BERT 시리즈, RoBERTa, DistilBERT, ALBERT 를 포함하며, 입력에 대한 임베딩(embedding)을 출력하여 다양한 후속 작업(downstream tasks)에 활용됩니다.
- 인코더-디코더 모델 (Encoder-decoder models): 원본 트랜스포머 아키텍처를 사용하며 MarianMT, T5, BART, mBART, mT5 와 같은 모델들이 있으며, 주로 번역이나 요약과 같은 작업에 사용됩니다.
- 디코더 전용 모델 (Decoder-only models): GPT 시리즈와 Llama 시리즈를 포함하며, 사용자의 질문에 대한 문장을 생성하는 데 사용됩니다.
- LLM의 규모 확장과 도전 과제
- LLM은 [3] 를 따르며, 그 규모가 점점 더 커지는 경향이 있습니다.
- 이로 인해 모델 추론(inference) 및 미세 조정을 위해 엄청난 양의 메모리 용량이 필요하다는 문제가 발생합니다.
- LoRA (Low-Rank Adaptation)를 통한 해결
- LoRA 는 이러한 문제를 극복하기 위해 사전 학습된 LLM을 미세 조정하는 데 주로 사용되는 파라미터 효율적인 미세 조정(parameter-efficient fine-tuning) 기법입니다.
- LoRA는 모델의 다른 모든 가중치를 고정하고, 어텐션 레이어와 같은 중요한 레이어에 LoRA 어댑터(adapter)를 추가하여 미세 조정을 수행합니다.
- 이 방법을 통해 전체 파라미터의 1% 미만만을 업데이트하여 LLM을 미세 조정할 수 있어 효율성이 크게 향상됩니다.
Privacy-preserving transformer using HE
- 대화형(Interactive) 시나리오
- 작동 방식: 보안 다자간 계산(Secure Multi-Party Computation, MPC)과 동형 암호(HE)를 결합합니다. 여러 당사자 간의 통신을 통해 암호화된 상태에서 계산을 수행합니다.
- 장점: 당사자 간의 통신을 통해 암호화된 계산 시간을 줄일 수 있습니다.
- 선행 연구: THE-X [4]: BERT-tiny 모델의 추론(inference)을 위한 최초의 프로토콜을 제안하며, HE 친화적인 워크플로우와 통신을 통한 비다항식 연산 평가 방법을 도입했습니다.
- 대화형 시나리오의 이후 연구에서는 계산 시간을 개선하고 통신 비용을 줄이는 데 집중했습니다.
- Limitations: 모델의 크기가 커질수록 대규모 통신에 어려움을 겪을 수 있으며, 계산이 진행되는 동안 데이터 소유자가 온라인 상태여야 한다는 제약이 있습니다.
- 비대화형(Non-interactive) 시나리오
- 작동 방식: 오직 동형 암호(HE)에만 의존하여 계산을 수행합니다. 데이터 소유자가 계산 중에 온라인 상태일 필요가 없습니다.
- 장점: 대화형 방식의 통신 및 온라인 상태 유지 요구 사항과 같은 한계를 해결합니다.
- 선행 연구
- [5]: HE 친화적인 트랜스포머 모델을 처음으로 소개했습니다. 기존 트랜스포머를 HE 친화적인 구조로 변경하고, 근사 도메인(approximation domain)을 최소화하며, 변경된 구조에 맞게 사전 학습된 가중치를 얻어 BERT 모델의 비대화형 추론을 수행했습니다.
- NEXUS [6]: 재학습 없이 비다항식 연산을 다항식 근사(polynomial approximation)로 대체하여 비대화형 BERT 추론 방법을 제안했습니다.
- Powerformer [7]: 이 논문과 유사하게 어텐션(attention) 레이어의 소프트맥스(softmax) 함수를 BRP-max 함수로 대체하여 동형 암호 추론을 제안했습니다.
- 미세 조정(Fine-tuning) 적용의 도전 과제: 미세 조정은 트랜스포머 모델을 개선하고 개인화된 응답을 제공하는 데 매우 중요합니다.
- 이전 연구들의 한계점
- 이전 연구들은 주로 "secure inference" 에 초점을 맞추었으며, 특히 비대화형 환경에서 미세 조정의 상당한 계산 복잡성 때문에 이 문제를 회피하는 경향이 있었습니다.
- 일부 시도 [8,9] 가 있었지만, 주로 분류 헤드(classification head) 에만 집중하고 어텐션 레이어나 피드포워드 네트워크(feed-forward networks)와 같은 다른 핵심 구성 요소는 다루지 않았습니다.
- P3EFT [10]도 파운데이션 모델(foundation models)의 미세 조정을 다루지만, 주로 미세 조정 중 에너지 소비에 초점을 맞추었습니다.
- 본 연구의 기여 (Beyond inference): 이 논문은 LoRA 미세 조정과 가우시안 커널(Gaussian Kernel)을 활용하여 이러한 계산 병목 현상을 해결하고, 개인화된(개인) 미세 조정 후 추론에 중점을 둔 동형 암호(HE) 친화적인 트랜스포머 아키텍처를 제안하여 미세 조정의 문제를 해결합니다.
1.2 Contributions
- HE 친화적인 Transformer 아키텍처 제안: 이 논문은 LLM이 사용자 상호작용에 기반한 개인화된 응답을 제공할 때 발생하는 프라이버시 문제를 해결하기 위해 동형암호(HE)를 적용한 Transformer 모델 아키텍처를 제시합니다.
- 두 가지 computational bottlenecks 현상 해결
- 첫 번째 computational bottlenecks: 대규모 암호문-암호문 행렬 곱셈(CCMM) 회피
- LLM을 동형암호 환경에서 파인튜닝할 때, 사용자의 개인 데이터를 기반으로 하는 파인튜닝 업데이트는 암호화된 상태로 저장되어야 합니다. 이는 큰 규모의 암호문-암호문 행렬 곱셈(Ciphertext-Ciphertext Matrix Multiplications, CCMM)을 발생시키는데, CCMM은 계산 비용이 매우 높습니다.
- 이 논문에서는 LoRA (Low-Rank Adaptation) 파인튜닝 방식을 활용하여 이 문제를 해결합니다. LoRA는 전체 모델의 가중치를 업데이트하는 대신, 적은 수의 파라미터만을 효율적으로 업데이트하여 CCMM의 크기를 크게 줄여 계산 비용을 절감합니다.
- 두 번째 computational bottlenecks: Softmax 연산의 대체
- 동형암호는 기본적으로 다항식(polynomial) 연산만 지원합니다. 그러나 Transformer 모델의 Attention 메커니즘에서 중요한 Softmax 함수는 지수(exponential) 함수와 나눗셈(division)을 포함하는 비다항식 함수이므로, HE 환경에서 계산하기가 매우 어렵고 수치적으로 불안정할 수 있습니다.
- 이 논문에서는 Softmax 계층을 보다 간단한 가우시안 커널(Gaussian kernel, GK)로 대체합니다. GK는 나눗셈이나 max 함수와 같은 복잡한 비다항식 연산이 필요 없어 HE 환경에서 효율적으로 근사하고 계산할 수 있습니다.
- 첫 번째 computational bottlenecks: 대규모 암호문-암호문 행렬 곱셈(CCMM) 회피
- 실험 결과: HE 암호화된 BERT-스타일 Transformer 모델을 사용하여 실험한 결과, 기존 방식 대비 파인튜닝에서 6.94배, 추론에서 2.3배의 상당한 계산 속도 향상을 달성했습니다. 이러한 속도 향상에도 불구하고 평문(plaintext) 모델과 유사한 성능을 유지하는 것을 입증했습니다. 이는 데이터 보호가 중요한 분야에서 프라이버시를 보존하는 LLM 서비스 제공 가능성을 보여주는 중요한 증명입니다.
2 Server-Client Computation Model and Preliminaries
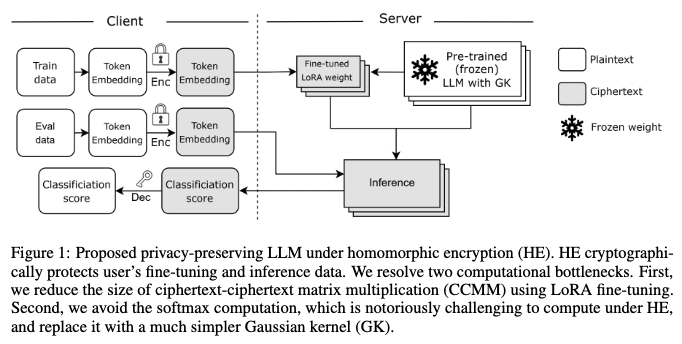
2.1 SERVER-CLIENT COMPUTATION MODEL
- 클라이언트
- 클라이언트는 개인 데이터(예: 사용자 상호 작용 기반의 개인화된 응답을 위한 데이터)를 보유합니다.
- 이 데이터를 CKKS (Cheon et al., 2017) 암호문으로 암호화하여 LLM 서비스 제공자인 서버로 전송합니다.
- 서버로부터는 암호화된 추론(inference) 결과를 받습니다.
- 서버 (Fine-tuning and Inference)
- 서버는 클라이언트로부터 암호화된 토큰 임베딩 데이터를 받아 파인튜닝(fine-tuning)을 수행합니다.
- 이 과정에서 사용자에게 맞춤화된 암호화된 LoRA 가중치(encrypted LoRA weights)를 생성합니다.
- 이후, 암호화된 추론 데이터와 함께 평문(plaintext) 상태의 사전 학습된 가중치(pre-trained weights) 및 암호화된 LoRA 가중치를 사용하여 추론을 수행합니다.
- 추론이 완료되면 암호화된 결과를 다시 클라이언트에게 반환합니다.
- 데이터 보호 및 보안 모델
- 본 모델은 "Semi-honest security model"을 기반으로 합니다. 이는 공격자(adversary)가 프로토콜을 충실히 따르지만, 모델에서 생성되는 모든 중간 및 최종 결과물을 수집할 수 있음을 의미합니다.
- 클라이언트의 입력 데이터는 CKKS 암호문으로 암호화되어 전송되기 때문에, 사용자 데이터는 LLM 서비스 제공자(서버)로부터도 암호학적으로 보호됩니다. 즉, 서버는 사용자 데이터를 평문 형태로 볼 수 없습니다.
- 전체 보안 모델은 기반이 되는 CKKS 암호화 방식의 "semantic security"에 의존합니다.
- 보호되지 않는 요소 및 한계
- 토큰 임베딩 레이어 가중치: 이 가중치는 암호화되지 않으며 파인튜닝 과정에서도 업데이트되지 않습니다.
- LLM 가중치 탈취 문제: 사전 학습된 LLM 가중치와 파인튜닝된 LoRA 가중치는 서버에 존재하며 사용자에게 공유되지 않지만, 본 논문의 접근 방식은 [11,12] 와 같은 연구에서 다루는 "모델 가중치 탈취 문제(model weight stealing problem)"를 직접적으로 해결하지는 않습니다. 즉, 모델 자체의 가중치가 암호학적인 의미에서 엄격하게 보호되는 것은 아닙니다.
2.2 HOMOMORPHIC ENCRYPTION AND CKKS
- 동형 암호(HE)
- 데이터를 암호화된 상태로 유지하면서도 계산을 수행할 수 있도록 하는 암호화 방식입니다.
- 이는 데이터를 복호화하지 않고도 암호문 상에서 직접 덧셈이나 곱셈 같은 연산을 할 수 있다는 의미입니다.
- 이러한 특성 덕분에 데이터 프라이버시를 보호하면서도 클라우드 서비스 등에서 기계 학습과 같은 연산을 수행할 수 있게 해줍니다.
- CKKS 스킴
- HE 방식 중 하나로, 실수를 암호화하는 데 특히 효율적입니다.
- 데이터 암호화 방식: 실수 또는 복소수 데이터를 다항식 형태로 암호화합니다.
- 근사 연산: 암호화된 데이터에 대해 '근사적인' 연산을 수행합니다. 이는 CKKS가 정확한 값을 계산하는 대신 근사치를 사용한다는 것을 의미하며, 이는 특정 오차 범위 내에서 결과를 허용하는 기계 학습과 같은 애플리케이션에 적합합니다.
- SIMD(Single Instruction Multiple Data) 지원: 여러 개의 실제 또는 복소수 데이터를 하나의 암호문에 '패킹'하여 저장할 수 있습니다. 이를 통해 한 번의 연산으로 여러 데이터에 대한 계산을 동시에 수행하는 SIMD 연산을 지원하여 효율성을 높입니다.
- Plaintext: HE와 관련하여 "plaintext"는 암호화되지 않은 다항식을 의미하며, 이 다항식은 메시지 벡터를 포함합니다.

- CKKS의 레벨(Level)
- 정의: CKKS 암호문에는 제한된 수의 곱셈 연산(Mult, pMult)이 허용됩니다. 이 허용되는 곱셈 횟수를 '레벨'이라고 하며, 암호화가 시작될 때 결정됩니다.
- 모듈러스(Modulus) Q 감소: 암호화된 데이터에 대해 곱셈 연산을 수행할 때마다, 암호문의 연산 정밀도와 관련된 모듈러스 Q 값이 감소합니다. 이는 암호문이 '노이즈'를 축적하는 과정과 관련이 있습니다.
- 레벨 예산 소진: 만약 곱셈 연산이 너무 많이 수행되어 모듈러스 Q가 충분히 커지지 않거나, 미리 정해진 '레벨 예산'이 소진되면 더 이상 유효한 곱셈 연산을 진행할 수 없게 됩니다.
- 부트스트래핑(Bootstrapping, BTS)
- 목표: '부트스트래핑'은 소진된 레벨 예산을 회복하고 암호문의 노이즈를 재설정하여 추가적인 곱셈 연산을 가능하게 하는 과정입니다 (Cheon et al., 2018).
- 높은 연산 비용: BTS는 현재까지 알려진 동형 암호 연산 중에서 가장 비용이 많이 드는 작업입니다. 본문에 따르면 일반적인 곱셈(Mult)이나 회전(Rot) 연산보다 100배 이상 느립니다.
- 알고리즘 설계의 중요성: 이러한 높은 비용 때문에, 동형 암호 기반의 애플리케이션(예: 개인 정보 보호 기계 학습)을 설계할 때 BTS의 사용을 최소화하는 것이 전체 연산 속도 향상에 결정적인 역할을 합니다.
- Challenges
- 레벨과 부트스트래핑의 특성 때문에, LLM과 같이 복잡하고 깊은 신경망에 동형 암호를 적용하는 것은 큰 도전 과제였습니다. 모델의 계산량이 많아질수록 더 많은 곱셈 연산이 필요하고, 이는 곧 잦은 부트스트래핑으로 이어져 연산 속도 저하를 야기하기 때문입니다.
- 이 논문은 LoRA와 Gaussian Kernel을 활용하여 이러한 computational bottlenecks 현상을 해결하려는 시도 중 하나입니다.
Matrix multiplications: PCMM and CCMM.
동형 암호(HE) 환경에서 트랜스포머 모델을 평가할 때, 행렬 곱셈에는 두 가지 주요 유형이 있습니다.
PCMM (Plaintext-Ciphertext Matrix Multiplication): 평문(암호화되지 않은 데이터) 행렬과 암호문(암호화된 데이터) 행렬 간의 곱셈을 의미합니다.
CCMM (Ciphertext-Ciphertext Matrix Multiplication): 두 암호문 행렬 간의 곱셈을 의미합니다.
- PCMM이 CCMM보다 빠른 이유
- 동형 암호 연산은 일반적인 평문 연산보다 훨씬 느립니다. 특히 Mult(암호문 간 곱셈) 및 Rot(회전)과 같은 연산은 pMult(평문-암호문 곱셈) 및 pRot(평문-암호문 회전)보다 훨씬 더 많은 계산 시간을 필요로 합니다 (표 5 참조).
- PCMM은 암호화되지 않은 평문 데이터를 사용하기 때문에 pMult와 pRot와 같은 상대적으로 빠른 연산을 활용할 수 있습니다. 반면, CCMM은 두 암호화된 데이터를 곱해야 하므로 더 느린 Mult 및 Rot 연산을 더 많이 사용해야 합니다.
- JKLS 알고리즘 [13] 을 통한 효율성 개선
- 이 논문에서는 동형 행렬 곱셈의 효율성을 높이기 위해 JKLS 알고리즘을 사용합니다. 이 알고리즘은 행렬 요소가 단일 암호문에 패킹될 수 있을 때 가장 빠른 HE 계산 알고리즘을 제공합니다.
- 대규모 행렬 처리: 행렬의 크기가 가용한 암호문 공간보다 큰 경우, JKLS 알고리즘은 '블록 단위 행렬 곱셈(block-wise matrix multiplication)'을 반복하여 대규모 행렬 곱셈을 평가할 수 있도록 합니다.
- 계산 시간 격차: 이 블록 단위 연산으로 인해 PCMM과 CCMM 간의 계산 시간 격차는 블록 행렬의 수에 비례하게 됩니다. 이는 큰 모델에서 CCMM의 계산 비용이 더욱 커진다는 것을 의미합니다.
Polynomial approximations of non-polynomial functions.
- 다항식 연산에 대한 지원: HE의 핵심 원리는 데이터를 다항식 형태로 암호화하고, 이 다항식에 대해 덧셈과 곱셈 같은 기본적인 대수적 연산을 수행하는 것입니다. 이는 암호화된 데이터에 대한 연산이 복호화 없이도 가능하다는 것을 의미합니다.
- 비다항식 연산의 한계: 그러나 나눗셈, 최댓값(max) 함수, 지수 함수(exponential function)와 같은 비다항식 연산들은 HE 환경에서 직접적으로 지원되지 않습니다. 이러한 연산들은 일반적으로 비교(comparison)나 조건문(if-statements)을 포함하며, 이는 다항식 연산으로 표현하기 어렵습니다.
- 다항식 근사의 필요성: 따라서, HE를 사용하여 실제 기계 학습 모델을 실행하기 위해서는 이러한 비다항식 연산들을 다항식으로 근사해야 합니다. 예를 들어, Softmax 함수 내의 지수 함수나 Layer Normalization 및 AdamW 옵티마이저에 사용되는 역제곱근 함수 등이 여기에 해당합니다.
- 근사의 복잡성: 이러한 다항식 근사의 복잡성(예: 다항식의 차수, 연산 시간)은 근사하려는 함수의 입력 범위와 특성에 크게 의존합니다. 입력 범위가 넓거나 함수의 변화가 급격할수록 더 높은 차수의 다항식이 필요하며, 이는 계산 비용 증가로 이어집니다.
- CKKS 스킴: 이 논문에서 사용하는 CKKS 는 실수 또는 복소수 데이터를 근사적으로 암호화하고 연산하는 데 효율적인 HE 스킴으로, 이러한 다항식 근사의 중요성을 더욱 부각시킵니다.
- Approach
- 이 논문에서는 HE 환경에서의 계산 병목 현상을 해결하기 위해 Softmax 함수를 다항식으로 근사하기 더 쉬운 Gaussian kernel(GK)로 대체하는 방법을 제안했습니다.
- 이는 HE가 다항식 연산만 지원한다는 근본적인 제약을 극복하고, 실제 LLM 추론 및 미세 조정을 가능하게 하는 중요한 진전입니다.
- Related Works
- 주로 안전한 추론에 초점을 맞추었으며, 미세 조정의 복잡성 때문에 이를 회피하는 경향이 있었습니다.
- Powerformer [7]: 이 논문과 유사하게 Softmax를 BRP-max 함수로 대체하여 동형 암호화된 환경에서의 추론을 개선하려는 시도입니다.
- HETAL [9]: HE 기반의 효율적인 전이 학습을 다루며, 특히 분류 헤드 부분의 미세 조정에 집중합니다.
2.3 LARGE LANGUAGE MODELS, ATTENTION LAYERS, AND LORA FINE-TUNING
- 어텐션 메커니즘 (Standard Attention Mechanism)
- 트랜스포머 모델의 기본 구성 요소인 어텐션은 입력 시퀀스의 다른 부분과 관련된 정보를 통합하는 데 사용됩니다.
- 입력: 어텐션 메커니즘은 세 가지 주요 행렬, 즉 Query (Q), Key (K), Value (V)를 사용합니다.

- Attention score
- 이는 각 쿼리와 모든 키 간의 유사도 점수(similarity score)를 계산하는 과정입니다. 이 점수는 각 쿼리 단어가 시퀀스의 다른 단어들과 얼마나 관련되어 있는지를 나타냅니다.
- sqrt{n}: 계산된 유사도 점수를 임베딩 차원의 제곱근인 sqrt{n} 으로 나눕니다. 이는 스케일링(scaling) 과정으로, 점수가 너무 커지는 것을 방지하여 Softmax 함수의 기울기(gradient)가 너무 작아지는(vanishing) 문제를 완화하고 학습 안정성을 높이는 데 기여합니다.
- Softmax: 스케일링된 유사도 점수에 Softmax 함수를 행(row) 단위로 적용합니다. Softmax는 각 점수를 0과 1 사이의 확률 분포로 변환하여, 해당 쿼리에 대해 각 키가 얼마나 중요한지(가중치)를 나타냅니다.
- V: Softmax를 통해 얻은 가중치(확률 분포)를 Value 행렬 V 에 곱합니다. 이는 가중치에 따라 각 값 벡터를 합산하여, 해당 쿼리 단어에 대한 최종적인 어텐션 출력(context vector)을 생성합니다. 이 출력은 입력 시퀀스 전체에서 해당 쿼리에 중요한 정보를 담고 있습니다.
- Computational complexity: 이 논문에서는 동형 암호화(Homomorphic Encryption, HE) 환경에서 Softmax 함수가 계산적으로 어렵다는 점을 언급하며, 이는 이후 섹션에서 Softmax를 Gaussian Kernel(GK)로 대체하는 이유를 제시합니다.
- LoRA (Low-Rank Adaptation) [1]
- LoRA는 LLM의 미세 조정(fine-tuning)을 위한 매개변수 효율적인(parameter-efficient) 방법론으로, 특히 대규모 모델의 학습 부담을 줄이는 데 널리 사용됩니다.
- 목적: 기존의 사전 학습된(pre-trained) LLM의 모든 가중치를 미세 조정하는 대신, 적은 수의 추가 매개변수만을 학습하여 효율성을 높입니다.
- LoRA 동작 원리
- 신경망의 선형 레이어(linear layer)에 있는 기존 가중치 행렬 W 가 있다고 가정합니다.
- LoRA는 W 를 직접 업데이트하는 대신, W 에 낮은 랭크(low-rank) 업데이트 행렬인 ∆W = AB 를 추가합니다.
- 이러한 방식으로 선형 레이어의 동작은 입력 X 에 대해 X → X(W + AB) 가 됩니다.
- 미세 조정 과정에서 사전 학습된 W 는 고정(frozen)되고, 오직 두 개의 작은 행렬 A 와 B 만이 훈련됩니다.
- 장점: LoRA는 학습해야 할 매개변수의 수를 크게 줄여, 미세 조정에 필요한 계산 자원(메모리, 연산 시간)을 절감하는 동시에 모델 성능을 유지하는 데 효과적입니다. 이 논문에서는 특히 동형 암호화 환경에서 LoRA가 대규모 암호문-암호문 행렬 곱셈(CCMM)을 피하고 계산 속도를 향상시키는 데 기여한다고 강조합니다.
3 SPEEDUP WITH LORA: AVOIDING LARGE CCMM
Bottleneck 1: Full fine-tuning incurs large CCMM.
- 프라이버시 보호의 필요성: 사용자의 개인화된 파인튜닝 데이터는 암호화된 상태로 서버에 전송됩니다. 이 데이터에 기반한 파인튜닝 업데이트 ∆W 또한 암호화된 상태로 저장되어야 합니다.
- 선형 레이어 계산의 문제: 선형 레이어의 연산은 입력 X와 가중치 W를 사용하여 XW 형태로 계산됩니다. 파인튜닝을 통해 가중치가 W + ∆W로 업데이트되면, 계산은 X(W + ∆W) = XW + X∆W가 됩니다.
- PCMM vs. CCMM
- PCMM (Plaintext-Ciphertext Matrix Multiplication): XW 연산에서 입력 X는 암호화되어 있지만, 사전 학습된 가중치 W는 평문(암호화되지 않은 상태)으로 서버에 존재합니다. 따라서 이 연산은 평문-암호문 행렬 곱셈(PCMM)으로 처리될 수 있습니다. PCMM은 상대적으로 계산 비용이 저렴합니다.
- CCMM (Ciphertext-Ciphertext Matrix Multiplication): X∆W 연산에서 입력 X와 파인튜닝 업데이트 ∆W는 모두 암호화되어 있습니다. 암호화된 두 행렬을 곱하는 것은 암호문-암호문 행렬 곱셈(CCMM)이며, 이는 PCMM에 비해 훨씬 계산 비용이 비쌉니다.
- 전체 파인튜닝의 문제점: "Full fine-tuning(전체 파인튜닝)"은 LLM의 모든 가중치를 업데이트하는 방식입니다. 이는 ∆W가 거대한 행렬이 되고, 따라서 수많은 X∆W와 같은 대규모 CCMM 연산이 발생하게 하여 엄청난 계산 비용을 초래합니다.
- 이러한 CCMM의 높은 계산 비용은 동형 암호 기반의 프라이버시 보존 머신러닝(PPML)에서 큰 병목 현상으로 작용합니다. 이 논문에서는 이를 해결하기 위해 LoRA 를 활용하여 ∆W의 크기를 줄여 CCMM 연산의 부담을 완화하는 방안을 제시합니다.
Accelerating homomorphic matrix-multiplication with LoRA.
- LoRA의 일반적인 이점: 일반적인 평문(plaintext) 환경에서 LoRA의 주된 이점은 옵티마이저 메모리 상태가 적어 메모리 사용량을 줄이는 것입니다. 즉, 모델 전체의 가중치를 업데이트하는 대신, 작은 크기의 LoRA 어댑터만 업데이트하여 메모리 효율성을 높입니다.
HE 환경에서의 LoRA 이점: 하지만 동형 암호 환경에서는 LoRA의 주된 이점이 계산 비용 절감으로 바뀝니다. 특히, 계산 비용이 높은 Ciphertext-Ciphertext Matrix Multiplication (CCMM)을 Plaintext-Ciphertext Matrix Multiplication (PCMM)과 더 작은 크기의 CCMM으로 변환하는 데 기여합니다.
계산 과정 분석: 논문은 이를 설명하기 위해 선형 레이어의 업데이트를 다음과 같은 수식으로 표현합니다:
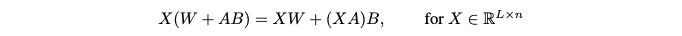
- X: 암호화된 입력 데이터입니다. 여기서 L 은 시퀀스 길이, n 은 임베딩 차원입니다.
- W: 사전 학습된 선형 레이어의 가중치 행렬이며, 이는 plaintext 상태로 서버에 저장됩니다.
- A, B: LoRA 업데이트 행렬입니다. A와 B 는 W 보다 훨씬 작은 저차원 행렬입니다. LoRA를 통해 미세 조정되므로 이 A 와 B 행렬은 암호화된 상태로 존재합니다.
- XW matrix: 이 항은 암호화된 입력 X 와 평문 가중치 W 의 곱으로, PCMM(Plaintext-Ciphertext Matrix Multiplication)으로 계산됩니다. PCMM은 CCMM보다 훨씬 빠릅니다. 이 계산의 비용은 O(n^2) 에 비례합니다.
- (XA)B matrix: 이 항은 A 와 B 가 암호화되어 있기 때문에 CCMM(Ciphertext-Ciphertext Matrix Multiplication)으로 계산되어야 합니다. 하지만 LoRA는 업데이트 ∆W = AB 를 단일 행렬로 직접 계산하는 대신, A와 B 라는 두 개의 작은 행렬의 곱으로 분리합니다.
- 먼저 X 와 A 를 곱하는 연산 XA 는 O(nr) 비용을 가집니다.
- 그다음 (XA) 의 결과와 B 를 곱하는 연산은 O(nr) 비용을 가집니다.
- 큰 크기의 ∆W 를 직접 암호화하고 이를 CCMM으로 계산하는 것 O(n^2) 비용보다, A 와 B 를 사용하여 (XA)B 를 두 번의 작은 CCMM(즉, O(nr) 비용) 으로 계산하는 것이 훨씬 효율적입니다.
- LoRA는 암호화된 미세 조정 업데이트(A와 B)를 적용할 때 발생하는 대규모 CCMM을 피함으로써 동형 암호 계산의 병목 현상을 해결하고, 계산 속도를 크게 향상시킵니다. 이는 Table 1a와 Appendix G에 제시된 실험 결과에서 뚜렷한 계산 비용 차이로 나타납니다.
Reducing optimizer states and inverse square root with LoRA.
- 비다항식 함수와 HE의 한계: 동형 암호는 암호화된 상태에서 다항식 연산(덧셈, 곱셈 등)만을 지원합니다. 그러나 1/sqrt{x}와 같은 역제곱근 함수는 비다항식 함수이기 때문에 HE 환경에서 직접 계산하기 매우 어렵습니다.
- 부트스트래핑(Bootstrapping, BTS)의 필요성: 1/sqrt{x}와 같은 비다항식 함수를 HE에서 처리하려면, 일반적으로 근사를 통해 다항식 형태로 변환해야 합니다. 이 과정에서 넓은 입력 범위를 처리하거나 정확도를 유지하기 위해 부트스트래핑(Bootstrapping, BTS) 이라는 고비용의 HE 연산이 필요합니다. BTS는 다른 HE 연산(곱셈, 회전 등)보다 100배 이상 느리므로, 잦은 사용은 전체 계산 시간에 심각한 병목 현상을 초래합니다.
- 옵티마이저의 계산 병목: LLM은 매우 많은 파라미터를 가지고 있으며, AdamW와 같은 적응형 옵티마이저(adaptive optimizer)는 각 파라미터 업데이트 시 역제곱근 연산을 포함합니다. 이로 인해 전체 미세 조정(full fine-tuning) 시 옵티마이저의 계산 시간이 Transformer 블록 평가 시간을 초과할 정도로 전체 계산 시간의 큰 부분을 차지하게 됩니다.
- LoRA를 통한 병목 완화: LoRA 는 사전 학습된 모델의 모든 가중치를 업데이트하는 대신, 중요 계층(예: 어텐션 계층)에 작은 저랭크(low-rank) 어댑터(adapter)를 추가하여 이들만 미세 조정하는 방식입니다.
- 이는 미세 조정되는 파라미터의 수를 획기적으로 줄여줍니다. 예를 들어, 2-layer BERT 모델의 경우 전체 미세 조정 시 368개의 암호화된 가중치(ciphertext)가 필요했지만, LoRA를 사용하면 단 15개만 필요합니다.
- 결과적으로, AdamW 옵티마이저에서 필요한 1/sqrt{x}와 같은 역제곱근 연산 횟수가 대폭 감소하여 옵티마이저 계산 시간을 크게 줄일 수 있습니다. 이는 전체 미세 조정 및 추론 속도 향상에 기여합니다.
4 SPEEDUP WITH GAUSSIAN KERNEL: POLY-APX-FRIENDLY DESIGN
Bottleneck 2: Softmax is hard to evaluate under HE.
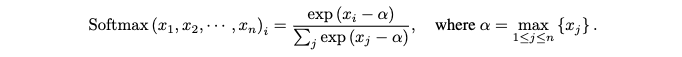
- 동형 암호(Homomorphic Encryption, HE) 환경: HE 에서는 다항식 연산만을 지원 (덧셈,곱셈) 하기 때문에, Softmax 함수를 평가하는 것이 어려운 과제입니다.
- 비다항식 함수의 포함: Softmax 함수는 위의 수식으로 정의됩니다.
- Softmax 함수는 다음과 같은 비다항식 함수들이 포함되어 있어 HE 환경에서 직접 적용하기 어렵습니다.
- 지수 함수 (exp): exp(x)는 비다항식 함수이므로 다항식으로 근사해야 합니다.
- 나눗셈: 분모에 있는 합으로 나누는 나눗셈 연산 또한 비다항식 함수이므로 근사가 필요합니다.
- Max 함수 (max): 전통적으로 (alpha) 값을 찾기 위해 사용되는 (max) 함수는 비교(comparison) 및 조건문(if-statement)을 통해 작동합니다. 이러한 논리적 연산은 HE에서는 비다항식으로 간주되므로, 이 역시 다항식 근사가 요구됩니다.
- 수치적 안정성 문제와 HE의 제약
- 일반적인 Softmax 계산에서 alpha 를 빼는 이유는 큰 양수의 지수 계산으로 인해 발생할 수 있는 수치적 불안정성(numerical instabilities)을 피하기 위함입니다. 그러나 HE 환경에서 이 alpha 값을 계산하는 것 자체가 어렵습니다.
- 이러한 비다항식 함수들을 HE에서 효율적으로, 그리고 정확하게 다항식으로 근사하는 것은 현재까지도 수치적으로 큰 도전 과제로 남아 있습니다.
- 이 논문에서는 이러한 Softmax 함수의 HE 적용 어려움을 해결하기 위해 Softmax 함수 대신 가우시안 커널(Gaussian Kernel, GK)을 도입하여 Softmax 계산의 병목 현상을 해소하고 계산 속도를 향상시켰습니다.
GK attention.
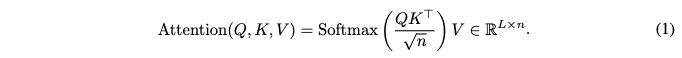
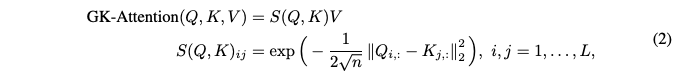
- Softmax 함수의 한계: 표준 어텐션 레이어 (1)은 Softmax 함수를 사용하여 어텐션 스코어를 얻습니다. 하지만 Softmax 함수는 HE 환경에서 지수 함수, 나눗셈, 최댓값 함수와 같은 비다항식 연산을 포함하고 있어 근사화하기 매우 어렵습니다.
- Gaussian Kernel 어텐션 제안: 이 논문에서는 Softmax 대신 Gaussian Kernel 을 사용하는 대안적인 어텐션 메커니즘인 GK-Attention을 제안합니다.
- Gaussian Kernel 의 이점
- 나눗셈 불필요: 1/sqrt{n} 은 고정된 상수이므로 미리 계산하여 곱할 수 있어, Softmax의 분모에 필요한 복잡한 나눗셈 연산이 필요 없습니다.
- Max 함수 불필요: Softmax 와 달리 최댓값 함수를 계산할 필요가 없어, HE에서 근사화하기 어려운 이 부분을 피할 수 있습니다.
- 지수 함수의 근사화 용이: exp(x)는 특정 범위에서만 근사화하면 되므로, 값이 발산하지 않아 수치적으로 훨씬 안정적이고 정확하게 근사할 수 있습니다.
- GK-Attention 관련 연구
- 암호화나 프라이버시와 관련 없는 분야에서도 기존 연구들이 유사한 아이디어를 제시했습니다.
- [14] 는 어텐션 레이어에서 정규화(나눗셈)가 불필요하다는 점을 지적하여 Transformer의 이론적, 실제적 특성을 개선했습니다.
- [15,16] 는 Softmax 대신 Gaussian Kernel 을 사용했으며, 특히 긴 컨텍스트 길이(context length)를 수용하기 위해 Gaussian Kernel 의 저랭크(low-rank) 근사를 활용하여 선형 복잡도 어텐션 레이어를 제시했습니다.
5 EXPERIMENTAL RESULTS
5.1 EXPERIMENTAL SETUP
Implementation of homomorphic encryption (HE).
- 동형 암호화(HE) 구현
- 기반 라이브러리: 이 연구의 HE 구현은 C++ 기반의 HEaaN 라이브러리를 사용했습니다.
- 하드웨어: 모든 실험은 8개의 Nvidia GeForce RTX 4090 24GB GPU를 활용했습니다.
- CKKS 스킴: CKKS 스킴의 FGb 파라미터를 사용했으며, 이는 최대 L=9 번의 곱셈 (Mult) 또는 pMult 연산을 부트스트래핑(Bootstrapping, BTS) 없이 수행할 수 있음을 의미합니다.
- 부트스트래핑(BTS) 연산
- BTS는 암호화된 상태에서 연산을 계속하기 위해 "레벨(level)"이라는 제한된 연산 횟수를 재충전하는 과정입니다. 이 논문에서는 최소 3레벨이 필요하다고 언급됩니다.
- 일반적인 BTS의 입력 범위는 [-1, 1] 이며, 이 범위를 초과하면 확장된 부트스트래핑 알고리즘인 ExtBTS 가 필요합니다. ExtBTS 는 더 넓은 입력 범위 [-2^{20}, 2^{20}] 를 지원하지만, 최소 4레벨을 요구합니다.
- 연산 속도
- 암호문-암호문 곱셈 Mult 은 평문-암호문 곱셈 pMult 보다 약 6배 느립니다.
- 암호문 회전 Rot (Rotation) 은 평문 회전 pRot 보다 약 24배 느립니다.
- 이러한 속도 차이가 암호문-암호문 행렬 곱셈(CCMM)이 평문-암호문 행렬 곱셈(PCMM)보다 훨씬 느린 주된 이유입니다.
Architecture.
- LLM 아키텍처
- 모델 유형: BERT 스타일의 인코더-온리(encoder-only) 트랜스포머 모델을 사용했습니다.
- 수정 사항: 트랜스포머 블록의 선형 레이어에서 모든 바이어스(bias) 항을 제거했습니다.
- 하이퍼파라미터
- 임베딩, 어텐션 레이어, FFN(Feed-Forward Network)의 히든 차원은 768이고, 어텐션 헤드 수는 12개입니다.
- FFN 구조: FFN에서는 히든 차원을 3072로 확장한 후, GLU(Gated Linear Unit) 및 ReLU를 사용하여 768로 다시 줄였습니다.
- 분류 헤드(Classification Head): BERT에 연결된 분류 헤드의 댄스 레이어(dense layer)를 (768, 1024) 형태에서 (768, 32)와 (32, 1024) 두 개의 블록으로 수정하여, HE 환경에서 더 최적화된 CCMM을 사용할 수 있도록 했습니다.
- 트랜스포머 레이어 수: 실제 계산 시간을 고려하여 트랜스포머 레이어는 2개로 설정했습니다.
- LoRA 적용: 파인튜닝 시 LoRA 는 쿼리(query), 값(value), 키(key) 레이어에만 적용했으며, 다른 레이어(e.g., FFN)에는 성능 향상이 미미하여 적용하지 않았습니다. 모든 LoRA 레이어의 랭크는 2입니다.
Non-polynomial approximation.
- HE는 다항식 연산만 지원하므로, 나눗셈, max 함수, exp 함수 등과 같은 비-다항 함수는 다항식으로 근사해야 합니다.
- 사용된 근사 방법: Remez approximation, Newton's method, iterative method, 미니맥스 함수 구성(composition of minimax functions)이 사용되었습니다.
- 도구: Remez 알고리즘은 Sollya tool 를 사용하여 계산되었습니다.
- 역제곱근 함수: 역제곱근 함수는 Remez 근사에 몇 단계의 뉴턴 방법을 결합하여 근사했습니다. 이는 추가적인 곱셈 깊이를 발생시키지만 더 빠른 근사를 제공합니다.
5.2 TIME MEASURMENTS
CCMM vs. PCMM.

Softmax vs. GK.
- 실험 설정 및 결과 요약
- 해당 비교는 입력 범위가 (-2^{10}, 0)인 조건에서 수행되었습니다.
- Softmax와 GK 모두 128x128 크기의 행렬 12쌍에 대해 연산을 수행했습니다.
- Softmax: HETAL [9] 방법을 사용하여 최댓값 함수, 지수 함수, 역수 함수를 동형적으로 근사하여 계산했습니다. 이 경우 8.99초가 소요되었습니다.
- Gaussian Kernel: 동일한 실험 설정에서 1.44초가 소요되어 Softmax보다 약 6.24배 더 빠른 연산 속도를 보였습니다.
Optimizer.

- Using AdamW-HE, a modified version of AdamW
- 두 가지 주요 수치적 어려움
- 비다항 함수 근사의 어려움: 동형 암호화는 기본적으로 다항 연산만을 지원합니다. 따라서 위 식에 포함된 제곱근과 1/x (역수)와 같은 비다항 함수는 다항식으로 근사해야 합니다. 이러한 근사는 특히 정교하게 수행하기 어렵습니다.
- 작은 epsilon 값으로 인한 역수 근사의 어려움: 일반적으로 epsilon 값은 10^{-12} 처럼 매우 작은 양수로 설정됩니다. 그러나 1/x 함수를 넓은 입력 범위에서 정확하게 근사하는 것은 매우 어렵습니다.
- 이러한 문제를 해결하기 위해, 본 논문에서는 AdamW의 8단계에 다음과 같은 수정을 제안합니다.
- 수정된 8단계:
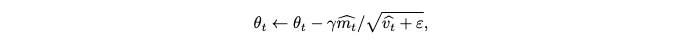
- epsilon 값 조정: 성능과 근사 정확도를 모두 고려하여 너무 작지 않은 적절한 \(\epsilon\) 값을 선택합니다.
- 최대 나누기 트릭(Maximum-dividing trick) 활용
- 특히 역제곱근 함수 1/sqrt{x}의 입력 범위를 제어하기 위해 다음과 같은 트릭을 사용합니다.
- 여기서 M 은 미리 정해진 값으로, x 가 1/sqrt{x} 의 근사 범위([0.0005, 1]) 안에 들어오도록 x 를 M 으로 나누어 조정합니다. 이를 통해 근사가 필요한 입력 범위를 좁히고, 1/sqrt{M} 은 미리 계산하여 곱할 수 있어 HE 환경에서의 계산 안정성을 높입니다.
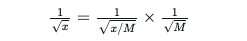
Computation time for our model and downstream tasks.
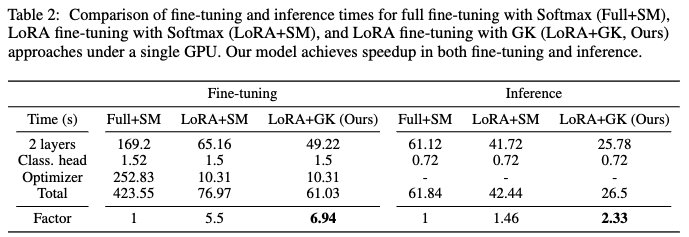
- Table 2: 이 표는 논문에서 제안하는 다양한 LLM 설정(Full+SM, LoRA+SM, LoRA+GK)에 대한 미세 조정(fine-tuning) 및 추론(inference)에 소요되는 시간을 비교 분석합니다.
- Baselines
- Full+SM (Full fine-tuning with Softmax): 일반적인 전체 미세 조정 방식과 Softmax 함수를 사용하는 모델입니다.
- LoRA+SM (LoRA fine-tuning with Softmax): LoRA (LoRA: Low-Rank Adaptation of Large Language Models) 미세 조정을 적용하고 Softmax 함수를 사용한 모델입니다.
- LoRA+GK (LoRA fine-tuning with Gaussian Kernel, Ours): 본 논문에서 제안하는 핵심 모델로, LoRA 미세 조정과 함께 Softmax 대신 Gaussian Kernel(GK)을 사용한 아키텍처입니다.
- 실험결과: 제안하는 방법 (LoRA+GK)은 미세 조정에서 Full+SM 모델 대비 6.94배 빠르고, 추론에서는 2.3배 빠른 속도 향상을 달성했습니다. 이는 동형 암호화(HE) 환경에서 LLM의 계산 효율성을 크게 개선했음을 보여줍니다.
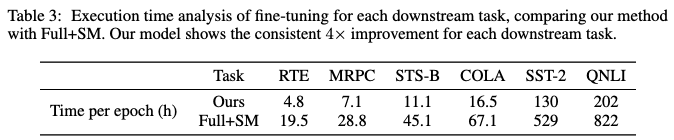
- Table 3
- 이 표는 GLUE 벤치마크에 포함된 다양한 다운스트림 작업(RTE, MRPC, STS-B, CoLA, SST-2, QNLI)에 대해 제안하는 모델(LoRA+GK)의 에포크(epoch)당 실행 시간을 Full+SM 모델과 비교합니다.
- 이는 downstream task 를 위한 fine-tuning 시간을 의미합니다.
- 제안하는 모델은 모든 다운스트림 작업에서 Full+SM 모델 대비 일관되게 약 4배의 속도 향상을 보여주었습니다.
5.3 DOWNSTREAM TASK PERFORMANCE ON ENCRYPTED LANGUAGE MODELS
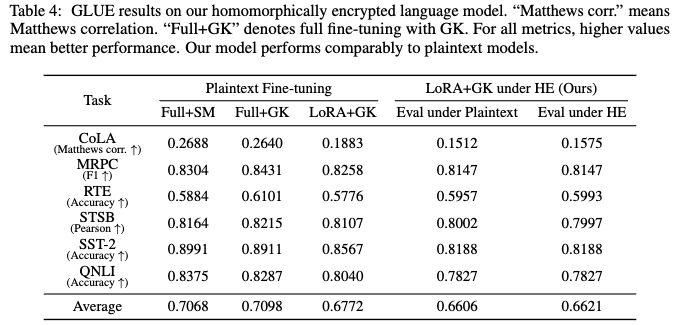
- GLUE 벤치마크 사용
- 본 연구에서는 모델의 성능을 평가하기 위해 GLUE(General Language Understanding Evaluation) 벤치마크를 활용했습니다.
- GLUE는 자연어 이해(NLU) 모델의 성능을 종합적으로 측정하는 데 사용되는 다양한 태스크들의 모음입니다.
- 하지만 WMNI, MNLI, QQP 는 모델 크기 및 계산 제약으로 인해 평가에서 제외되었습니다.
- Fine-tuning (미세 조정) 설정
- 손실 함수 (Loss Function)
- Cross-entropy loss: CoLA, MRPC, RTE, QNLI, SST-2 와 같은 분류(classification) 태스크에 사용되었습니다.
- MSE loss (Mean Squared Error loss): STSB 와 같은 회귀(regression) 태스크에 사용되었습니다.
- 에폭(Epoch)
- 계산 비용이 더 높은 SST-2 및 QNLI 태스크는 1 에포크만 Fine-tuning 했습니다.
- 다른 태스크들은 5 에포크 동안 Fine-tuning을 진행했습니다.
- 손실 함수 (Loss Function)
- 실험 조건 및 결과
- 옵티마이저 (Optimizer) 설정
- 평문(plaintext) 환경에서는 ε = 10^-12로 설정했습니다.
- 동형 암호(HE) 환경에서는 각 태스크에 따라 다른 ε 값을 사용했습니다.
- 반복 실험: 평문 실험의 경우 각 태스크를 10회 반복하여 가장 좋은 점수를 선택했습니다.
- 옵티마이저 (Optimizer) 설정
- Findings
- LoRA, Gaussian kernel, 그리고 동형 암호화를 적용했음에도 불구하고, 전체 Fine-tuning 방식(Full+SM)과 Softmax를 사용하고 암호화를 적용하지 않은 모델에 비해 모델 정확도 감소가 최소화되었습니다.
- 이는 프라이버시 보호를 위한 기술 적용이 성능 저하를 크게 일으키지 않음을 시사합니다.
6 CONCLUSION
- HE 친화적인 트랜스포머 아키텍처 (BERT-style LLM) 제안: 이 연구는 HE 환경에서 미세 조정(fine-tuning) 및 추론(inference) 시 속도 향상을 목표로 하는 수정된 트랜스포머 아키텍처를 제시합니다.
- 두 가지 주요 computational bottlenecks 현상 해결
- LoRA (Low-Rank Adaptation) 활용: LLM 미세 조정 시 발생하는 대규모 CCMM 문제를 해결합니다. LoRA는 업데이트해야 할 파라미터의 수를 현저히 줄여서, 값비싼 CCMM 연산을 더 작고 효율적인 PCMM 으로 전환하는 데 기여합니다.
- 가우시안 커널(Gaussian Kernel, GK) 도입: 어텐션(attention) 레이어에서 계산하기 어려운 Softmax 함수를 대신하여 가우시안 커널을 사용합니다. Softmax는 HE 환경에서 구현하기 복잡한 지수 함수(exponential function), 나눗셈(division), 최댓값 함수(max function)를 포함하므로, 이를 제거함으로써 계산 효율성을 크게 높입니다.
- 성능 향상: 암호화된 BERT 스타일 트랜스포머 모델을 사용하여 미세 조정에서 6.94배, 추론에서 2.3배의 상당한 속도 향상을 실험적으로 입증했습니다. 이는 일반 모델과 유사한 성능을 유지하면서 달성한 결과입니다.
- Future Works
- 암호화와 무관하게 작고 효율적인 언어 모델 훈련: 이는 HE 적용 여부와 관계없이 모델 자체의 효율성을 높이는 연구를 의미합니다.
- 기계 학습과 무관하게 HE의 기본 계산 원시 요소(computational primitives) 효율성 개선: 이는 HE 기술 자체의 계산 성능을 최적화하는 연구를 의미합니다.
- 암호화된 사용에 특화된 기계 학습 모델 개발: 이 논문에서 제시된 작업이 바로 이 세 번째 방향의 첫걸음이라고 명시하며, HE와 같은 암호화 기술의 특성을 고려하여 모델 아키텍처를 설계하는 연구를 강조합니다.
Reference
[1] LoRA: Low-Rank Adaptation of Large Language Models
[2] Attention is All you Need
[3] Scaling Laws for Neural Language Models
[4] THE-X: Privacy-Preserving Transformer Inference with Homomorphic Encryption
[5] Converting transformers to polynomial form for secure inference over homomorphic encryption (ICML 2024)
[6] Secure Transformer Inference Made Non-interactive
[7] Powerformer: Efficient privacy-preserving transformer with batch rectifier power max function and optimized homomorphic attention
[8] Privacy-preserving text classification on BERT embeddings with homomorphic encryption (NAACL 2022)
[9] HETAL: Efficient privacy-preserving transfer learning with homomorphic encryption (ICML 2023)
[10] PrivTuner with Homomorphic Encryption and LoRA: A P3EFT Scheme for Privacy-Preserving Parameter-Efficient Fine-Tuning of AI Foundation Models
[11] Stealing Machine Learning Models via Prediction APIs
[12] Stealing Part of a Production Language Model
[13] Secure Outsourced Matrix Computation and Application to Neural Networks
[14] Normalized Attention Without Probability Cage
[15] SOFT: Softmax-free Transformer with Linear Complexity
[16] Skyformer: Remodel Self-Attention with Gaussian Kernel and Nyström Method