Traditional Topic Model
1. Non-negative Matrix Factorization based topic model
2. (Bayesian) Probabilistic graphical model : LDA (Latent Dirichlet Allocation)
2-1. 디리클레 분포
디리클레 분포는 베타분포를 일반화한 형태로 0과 1사이의 값을 가지는 multivariate 확률변수의 bayesian 모형에 사용한다.
디리클레 분포의 probability density function (PDF) 는 다음과 같다.
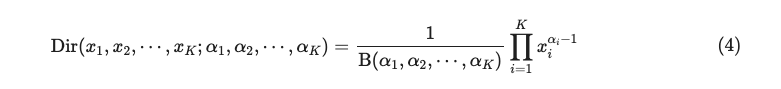
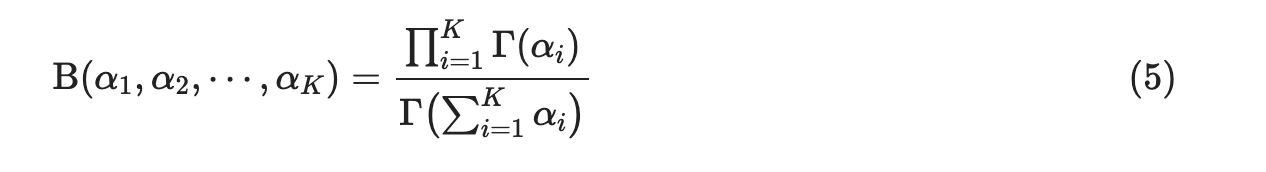
2-2. LDA Process ( Generative process + Inference process )
LDA 는 전통적인 토픽모델링 기법으로 , 우리의 목표는 토픽별 단어의 분포(Topic-Word distribution) 와 문서별 토픽의 분포(Document-Topic distribution) 두가지 분포를 모두 추정하는것이다.
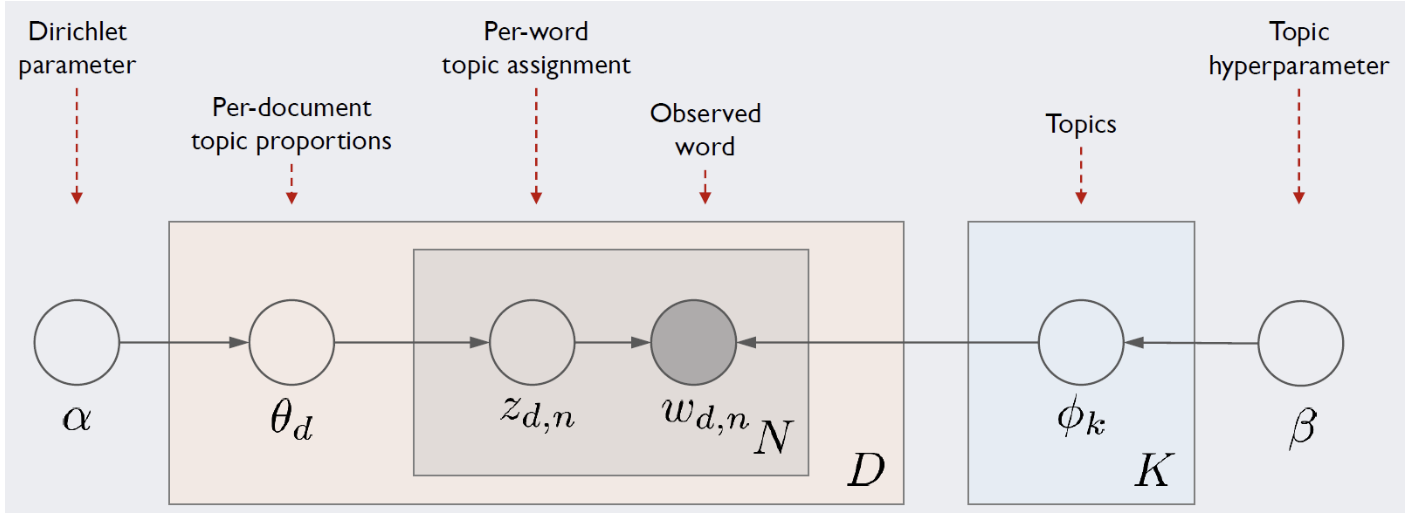
- Notation
D : 문서의 총 개수
K : 토픽의 총 개수
N : d번째 문서의 총 단어 개수
Doc-Topic distribution

Topic-Word distribution
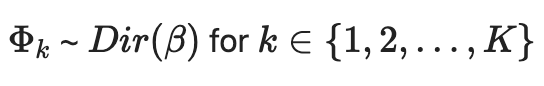
해당 단어의 토픽 분포
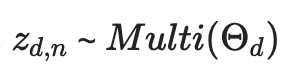
d 번째 문서의 n 번째 단어
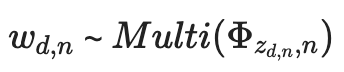
- LDA process 간단정리
corpus 내에 어떤 문서에 대해 각 문서당 토픽분포 (Doc-Topic distribution , 문서-토픽분포) 가 있다
앞에서부터 단어를 하나씩 채울때마다 문서-토픽분포로부터 하나의 토픽을 선택한다
다시 그 토픽으로부터 단어를 선택하고 다시 앞에서부터 반복하는 방식으로 문서 생성 과정을 모델링한다.
따라서 단어를 차례차례 하나씩 관측하며 "단어의 토픽분포" 를 갱신하고 그때마다 우리가 추정하는 두 분포인 Doc-Topic 분포와 Topic-Word 분포를 업데이트 하는과정을 거칩니다.
베이즈 정리의 관점에서 ,
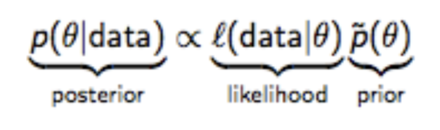
우리는 위와 같이 likelihood 가 다항분포를 따르는 상황 에서 , posterior 를 최대로 하는 prior 를 구하여 업데이트 해야하는데 이때 prior 와 posterior 가 동일한 분포를 따르면 그 과정이 쉬워집니다. 이때 prior 와 posterior 의 분포를 likelihood 의 conjugate prior 라고 하는데 다항분포의 conjugate prior 가 바로 디리클레분포입니다.
이때 posterior 를 최대로 하는 z 를 찾는 방법으로 이용하는것이 Gibbs sampling(MCMC) 혹은 Variational inference 입니다.
--------------------------------------------------------------------------------------------------------------
--> LDA 가 매우 훌륭한 모델이지만 , 몇몇 한계점 때문에 Neural Topic Model 에 대한 연구가 시작됐다.
1) 첫번째 문제는 , LDA inference process 에서 corpus 의 규모가 커질수록 계산량이 너무 많다는 문제이다.
이는 Gibbs sampling 혹은 기존 Variational inference 기법의 한계입니다.
2) 기존의 LDA 의 inference process 는 large text 로 확장해서 GPU 를 통한 컴퓨팅이 어렵다.
--> 이런 이유들로 , Deep Neural Networks (DNN) 에서 neural variational inference 를 이용한 VAE 기반의 NTM 연구가 발전되었습니다.