[Paper Review] Distributional Learning of Variational AutoEncoder: Application to Synthetic Data Generation (Neurips 2023)

Distributional Learning of Variational AutoEncoder: Application to Synthetic Data Generation
(Neurips 2023)
Seunghwan An, Jong-June Jeon
Abstract
- 기존의 일반적인 VAE의 한계: 기존 VAE는 계산 효율성이 좋음에도 불구하고, 잠재 공간에서 데이터가 가우시안 분포를 따른다는 가정이 주요 단점으로 지적되었습니다. 이 가정 때문에 모델이 복잡한 데이터 분포를 정확하게 포착하는 데 제약이 있었습니다.
- 제안하는 접근 방식 DistVAE: 이 논문에서 제안하는 DistVAE 는 디코더에 비대칭 라플라스 분포 (asymmetric Laplace distribution)의 무한 혼합(infinite mixture)을 사용합니다. 이 방식은 연속 변수에 대한 일반적인 분포 근사 능력을 가지고 있어 모델의 표현력을 크게 향상시킵니다.
- 이론적 기반: 제안된 모델은 일반적인 quantile function을 추정하기 위한 비모수 M-추정량(nonparametric M-estimator)의 특별한 형태로 표현됩니다. 이를 통해 모델과 quantile estimation 간의 관련성을 이론적으로 확립했습니다.
- 활용 및 장점: 제안된 모델은 합성 데이터 생성에 적용되었으며, 특히 데이터 프라이버시 수준을 쉽게 조정할 수 있다는 장점을 보여주었습니다.
1 Introduction
- VAE와 GAN의 분포 가정 차이: GAN은 adversarial loss 을 사용하여 실제 데이터 분포와 생성 모델의 분포 간의 Jensen-Shannon divergence 을 직접 최소화합니다. 이는 특정 분포에 대한 가정을 하지 않는 비모수적인(nonparametric) 방식으로 볼 수 있습니다.
- VAE에서 가우시안 분포 가정의 장점
- 재구성 손실(reconstruction loss): 데이터를 복원하는 과정에서 발생하는 손실이 가장 흔한 최적화 이론 손실 중 하나인 평균 제곱 오차(Mean Squared Error, MSE)로 해석될 수 있습니다. 가우시안 분포 가정 하에서는 로그 우도(log-likelihood)를 최대화하는 것이 MSE를 최소화하는 것과 관련됩니다.
- 샘플 생성 용이성: 새로운 데이터를 생성하는 과정이 계산적으로 매우 간단합니다.
- KL-divergence 계산 용이성: 잠재 공간의 분포와 사전 분포(prior distribution) 간의 KL-divergence 계산이 단순한 닫힌 형태closed form 로 가능합니다. KL-발산은 두 확률 분포의 차이를 측정하는 지표로, 가우시안 분포 사이의 KL-발산은 평균과 분산만으로 간단히 계산될 수 있습니다.
- VAE에서 가우시안 분포 가정의 한계
- 가우시안 분포 가정은 생성 모델의 "분포 용량(distributional capacity)", 즉 데이터의 복잡한 분포를 표현하는 능력을 제한합니다. 이는 VAE의 주요 한계점으로 지적되어 왔습니다.
- 생성 모델이 두 가우시안 분포 곱의 주변화(marginalization) 형태로 제약되기 때문입니다. 데이터의 실제 분포가 가우시안 분포와 크게 다를 경우, 모델이 이를 제대로 학습하기 어렵습니다.
- Gaussianity assumption (가우시안 분포 가정)
- VAE 에서 가우시안 분포 가정: 모델의 특정 부분, 특히 VAE의 디코더(decoder)나 잠재 공간(latent space)의 분포가 가우시안 분포(정규 분포)를 따른다고 가정하는 것을 의미합니다.
- 가우시안 분포는 평균과 분산이라는 두 가지 모수만으로 정의되며, 수학적으로 다루기 쉽다는 장점이 있습니다. 하지만 실제 데이터 분포는 종종 여러 개의 봉우리(multi-modal)를 갖거나 비대칭적인 형태를 보이는 등 가우시안 분포보다 훨씬 복잡할 수 있습니다.
- 기존 VAE의 문제점: 계산 효율성에도 불구하고, 기존 VAE는 생성 모델이 두 가우시안 분포의 곱을 주변화(marginalization)하는 형태로 제한되어 있어 분포 표현 능력이 떨어집니다. "분포 표현 능력(distributional capacity)"이란 특정 데이터 분포를 얼마나 잘 나타낼 수 있는지를 의미합니다.
- 기존 개선 노력의 한계
- 합성 데이터 생성 분야에서 분포 표현 능력을 높이기 위해 [1,2]는 디코더에 다중 모드(multimodality)를 도입하는 혼합 가우시안(mixture Gaussian) 모델링을 제안.
- 이는 가우시안 가정의 장점을 유지하면서도 복잡한 분포를 다룰 수 있게 했지만, 논문의 저자들은 수치 실험을 통해 혼합 가우시안만으로는 복잡한 근본 분포를 포착하기에 불충분하다는 것을 발견했습니다.
- 제안하는 DistVAE 접근 방식
- 논문의 주요 기여는 Gaussianity 가정을 넘어서, 관찰된 데이터셋의 ELBO(Evidence Lower Bound) 최대화 목표를 유지하면서 조건부 누적 분포 함수(Conditional Cumulative Distribution Function, CDF)를 직접 추정하는 새로운 VAE 학습 방법입니다.
- 이는 생성 모델에 대한 비모수적 분포 가정(nonparametric distribution assumption)을 의미합니다. 저자들은 이러한 새로운 접근 방식을 "VAE의 분포 학습(distributional learning of the VAE)"이라고 부르며, 무한 개수의 조건부 분위수(conditional quantiles)를 추정함으로써 가능해진다고 설명합니다.
- CRPS 손실 함수 활용: 제안된 분포 학습 방법의 목적 함수는 CRPS(Continuous Ranked Probability Score) 손실 함수를 채택하여 분포학습을 적용하지만 일반적인 VAE 에서 가우시안 분포를 가정할 때 처럼 여전히 계산적으로 다루기 쉬운 이점이 있습니다.
- 제안된 프레임워크의 장점
- 재구성 손실(reconstruction loss)이 CRPS 손실과 동등하며, 이는 적절한 스코어링 규칙(proper scoring rule)입니다
- 새로운 샘플 생성은 역변환 샘플링(inverse transform sampling) 덕분에 여전히 계산적으로 간단합니다.
- KL-divergence 계산은 여전히 간단한 닫힌 형태(closed form)로 이루어집니다.
3 Proposal
3.1 Distributional Learning
- 비대칭 라플라스 분포(Asymmetric Laplace distribution, ALD) 를 이용한 모델링
- alpha: 비대칭성을 나타내는 파라미터
- beta: 스케일을 나타내는 파라미터
- x: An observation
- x 의 확률모델을 아래와 같이 정의합니다.
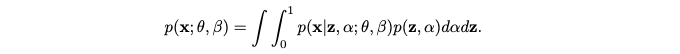
- 가정 1 (Assumption 1): 모델링의 단순화를 위해 몇 가지 독립성 가정이 도입됩니다.
- (1) 잠재 변수 z 가 주어졌을 때, 각 변수 x_j 들은 서로 조건부 독립입니다. 이는 변수들 간의 의존성을 오직 잠재 변수 z 를 통해 모델링함을 의미합니다.
- (2) 이산 변수(discrete variables) x_j 들은 파라미터 alpha 와 독립입니다. 이는 alpha 가 연속 변수(continuous variables)와만 관련됨을 시사합니다.
- (3) alpha 와 z 는 서로 독립입니다.
- Decoder 구조 (Equation 1): VAE 모델의 Decoder는 z 와 alpha 가 주어졌을 때 x 를 생성하는 확률 분포를 정의합니다. 가정 1에 따라, 이 분포는 연속 변수와 이산 변수에 대한 조건부 확률의 곱으로 표현됩니다.
- 연속 변수 j: 연속 변수의 조건부 확률은 ALD 형태로 표현됩니다.
- 이산 변수 j: 이산 변수의 조건부 확률은 z 에만 의존하며, 신경망 pi 를 통해 계산된 확률 분포에 따릅니다.
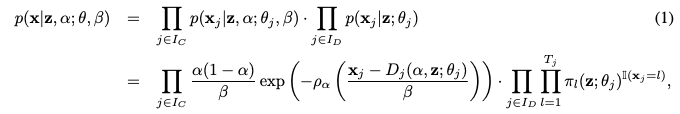
- 목적 함수 (Equation 2): DistVAE 모델은 이 목적 함수를 최소화하여 학습됩니다. 이 목적 함수는 VAE의 Evidence Lower Bound (ELBO)를 기반으로 유도됩니다.
- 첫 번째 항 (연속 변수): 연속 변수에 대한 재구성 손실(reconstruction loss)입니다. 이는 Continuous Ranked Probability Score (CRPS) 손실과 동일하며, 모델이 근본 분포의 누적 분포 함수(CDF)를 얼마나 잘 근사하는지를 측정합니다. CRPS 손실은 예측 분포와 실제 관측값 간의 거리를 측정하는 "적절한 스코어링 룰(proper scoring rule)" 중 하나입니다.
- 두 번째 항 (이산 변수): 이산 변수에 대한 재구성 손실입니다. 실제 값 x_j 에 해당하는 클래스의 예측 확률의 로그 값을 최대화(즉, 음수 로그 확률을 최소화)하는 형태입니다. 논문에서는 두 재구성 손실의 균형을 위해 두 번째 항의 beta 가중치를 제거했습니다.
- 세 번째 항: KL-divergence 항입니다. 데이터 x 가 주어졌을 때의 잠재 변수 사후 분포 posterior 가 사전 분포 prior 와 얼마나 다른지를 측정합니다. 이 항은 VAE의 정규화(regularization) 역할을 합니다.
- 여기서 beta 는 조절 가능한 상수로, ELBO 유도 과정에서 스케일링 팩터로 나타나며, 합성 데이터의 품질과 개인 정보 보호 수준 간의 trade-off를 조절하는 역할을 합니다.
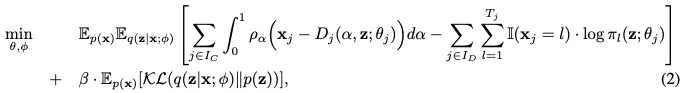
- 이론적 증명 1
- 유한 혼합 모델과의 연결 (Equation 3) & Theorem 1: 논문은 목적 함수 (2)가 유한 개수의 alpha_k 값을 가진 ALD 혼합 모델의 음수 ELBO를 스케일링한 값의 극한이라는 것을 보여줍니다.
- 유한 혼합 모델의 음수 ELBO (Equation 3)의 첫 번째 항은 특정 분위수 alpha_k 를 추정하기 위한 composite quantile loss로 해석될 수 있습니다. Theorem 1은 적분 조건을 만족하는 경우, K 를 무한대로 보낼 때 유한 혼합 모델의 재구성 손실이 CRPS 손실로 수렴함을 수학적으로 증명합니다. 이는 DistVAE가 분위수 추정을 통해 분포 학습을 수행함을 이론적으로 뒷받침합니다.
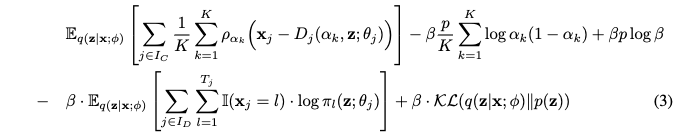
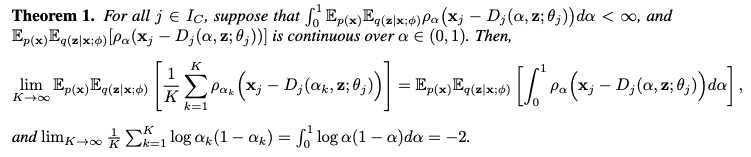
3.2 Theoretical Results
이 섹션에서는 DistVAE 모델이 원본 데이터의 실제 분포(ground-truth distribution)인 p(x)를 복구할 수 있는 이론적 근거를 설명합니다. 분석을 단순화하기 위해, 관측값 x가 p개의 연속 확률 변수(continuous random variables)로만 구성된 경우를 가정합니다. 특히 조건부 독립 가정과 분위수 추정과의 관련성을 강조합니다.
- Assumption 2: 이 논문에서 제안하는 DistVAE 모델의 특정 속성이 만족될 때 이론적인 결과가 성립함을 보장하는 가정을 명시합니다.
- (1) 주어진 임의의 phi 에 대해, 각 연속 변수 x_j 에 대한 조건부 누적 분포 함수(Conditional Cumulative Distribution Function, CDF) F_j 가 절대 연속(absolutely continuous)이고 모든 j 와 z 에 대해 엄격하게 단조 증가(strictly monotone increasing)함을 가정합니다. 이는 분위수 함수(quantile function)가 잘 정의되고 역함수를 가질 수 있게 합니다.
- (2) 주어진 임의의 theta 에 대해, 비대칭 라플라스 분포(Asymmetric Laplace Distribution, ALD)의 위치(location) 매개변수 함수 D_j 가 모든 j 와 z 에 대해 역함수(invertible)가 존재하고 미분 가능(differentiable)함을 가정합니다. 이는 ALD의 위치 매개변수가 분위수 함수와 직접적인 관계를 가질 수 있도록 합니다.
- (3) 응집된 사후 분포(Aggregated Posterior) q 가 잠재 변수의 사전 분포(Prior Distribution) p(z) 에 대해 절대 연속임을 가정합니다. 이는 학습된 사후 분포가 사전 분포와 특정 관계를 가짐을 의미합니다.
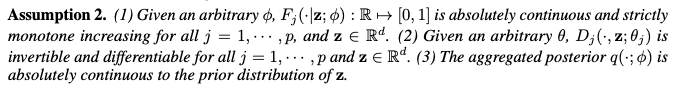
- Theorem 2는 이 조건부 PDF를 응집된 사후 분포에 대해 적분한 결과, 즉 모델이 생성한 데이터 분포가 실제 데이터 분포 p(x) 와 KL Divergence가 0이므로 같아진다는 것을 의미합니다. 이는 DistVAE가 데이터 재구성이 아닌, 실제 데이터 분포를 학습할 수 있는 이론적 능력을 가짐을 보여줍니다.
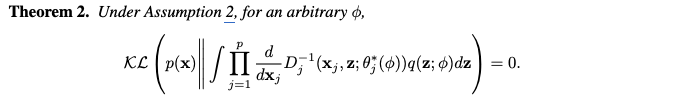
- Theorem 2 는 이론적으로 응집된 사후 분포 q 를 사용하여 실제 분포를 복원할 수 있음을 보이지만, q 는 계산이 어렵고 오버피팅을 유발할 수 있다는 단점이 있습니다. 이에 본 논문에서는 실제 합성 데이터 생성 과정에서는 q(z; phi) 대신 잠재 변수의 사전 분포 p(z) 를 사용하는 대안적인 접근 방식을 제안합니다. Equation 5와 6은 이 방법을 통해 얻어지는 추정된 PDF와 CDF를 정의합니다.
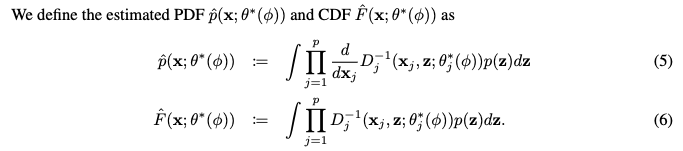
- Theorem 3 은 q(z; phi) 와 p(z) 간의 KL Divergence가 충분히 작을 때, 사전 분포 p(z) 를 사용한 추정된 PDF 역시 실제 분포 p(x)와 가까워질 수 있음을 이론적으로 뒷받침합니다. 이는 사전 분포를 사용하더라도 데이터 분포 학습이 가능하며, 계산 효율적인 합성 데이터 생성이 가능함을 시사합니다.
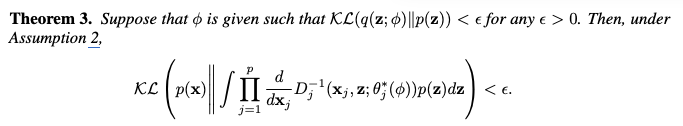
3.2.1 Synthetic Data Generation
본 논문에서 제안하는 DistVAE 의 data generation process 를 요약하면 아래와 같습니다.
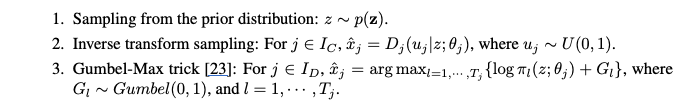
연속 변수와 이산 변수 모두 동일한 잠재 변수 z를 공유합니다. 이는 변수들 간의 종속성(dependency)을 포착하는 데 도움이 됩니다.
Gumbel-Max 트릭을 사용한 샘플링은 이산 변수의 레이블 불균형 비율(imbalanced ratio)을 유지하는 데 효과적이라고 합니다.
3.2.2 Parameterization of ALD
DistVAE 모델에서 연속 변수 x_j 에 대한 Asymmetric Laplace Distribution (ALD)의 위치 매개변수 D_j 를 선형 등경사 스플라인(linear isotonic spline) 방식을 사용하여 이 함수를 매개변수화합니다. 이는 D_j 가 분위수 함수(quantile function)의 역할을 할 수 있도록 보장하며, 계산의 효율성을 높입니다.
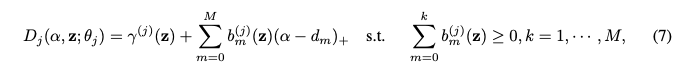
- 제안하는 매개변수화 방식의 핵심 이점
- 단조 증가성 보장: 등경사 제약을 통해 D_j 가 alpha 에 대한 유효한 분위수 함수가 되도록 합니다.
- 잠재 변수에 대한 의존성: gamma 와 b_m 가 잠재 변수 z 에 따라 달라지므로, 조건부 분위수 함수를 모델링하여 변수들 간의 의존성을 간접적으로 포착할 수 있습니다.
- 계산 효율성: 논문의 Appendix A.5에 설명된 바와 같이, 이 구조 덕분에 목적 함수 (2)의 재구성 손실(reconstruction loss)을 닫힌 형태(closed form)로 계산할 수 있어 학습이 용이합니다
4 Experiments
4.1 Overview
- 데이터셋: covertype, credit, loan, adult, cabs, kings 등 6가지 실제 테이블 형식 데이터셋을 사용했습니다. 데이터셋에 대한 자세한 설명은 Appendix A.8에 있습니다.
- Baselines: 제안된 DistVAE 모델은 최신 생성 모델인 CTGAN, TVAE, CTAB-GAN 과 비교했습니다.
4.2 Evaluation Metrics
- 머신러닝 유틸리티 (Machine Learning Utility, MLu)
- 합성 데이터를 학습시킨 모델의 예측 성능을 측정합니다.
- 사용된 모델: Linear (Logistic) Regression, Random Forest [6], Gradient Boosting [19].
회귀(regression) 작업에는 MARE(Mean Absolute Relative Error) [47]를, 분류(classification) 작업에는 F1 점수를 사용하여 성능을 평가합니다. MARE는 낮을수록, F1 점수는 높을수록 좋은 성능을 의미합니다.
- 통계적 유사성 (Statistical Similarity): 합성 데이터 분포가 실제 데이터 분포와 얼마나 유사한지를 측정합니다.
- 주변 분포(Marginal Distribution) 유사성: Kolmogorov statistic과 1-Wasserstein distance [18] 두 가지 지표를 사용합니다.
이 지표들은 실제 데이터와 합성 데이터의 경험적 주변 누적 분포 함수(Empirical Marginal CDFs) [40] 간의 거리를 측정합니다. 낮을수록 유사성이 높습니다. - 결합 분포(Joint Distribution) 유사성: 상관 행렬(correlation matrices)을 비교하여 평가합니다.
실제 데이터와 합성 데이터의 상관 행렬 간의 L2 거리를 계산합니다 (dython 라이브러리 사용). 낮을수록 유사성이 높습니다.
- 주변 분포(Marginal Distribution) 유사성: Kolmogorov statistic과 1-Wasserstein distance [18] 두 가지 지표를 사용합니다.
- 프라이버시 보존 능력 (Privacy Preservability): 합성 데이터가 실제 데이터의 프라이버시를 얼마나 잘 보호하는지를 측정합니다.
- Distance to Closest Record (DCR): 모든 실제 학습 샘플과 합성 샘플 간 L2 거리의 5번째 백분위수로 정의됩니다.
L2 거리 기반 지표이므로 연속형 변수에 대해서만 계산됩니다. DCR 값이 높을수록 프라이버시 보존 효과가 크다는 것을 의미합니다 (실제 데이터와 합성 데이터 간 겹침이 적음). 하지만 DCR 값이 지나치게 크면 생성된 합성 데이터의 품질이 낮을 수 있습니다. 따라서 DCR은 프라이버시 보존 능력과 합성 데이터 품질에 대한 통찰을 동시에 제공합니다. - 멤버십 추론 공격 (Membership Inference Attack): VAE 기반 합성기(DistVAE, TVAE 등)에 적용하기 위해 맞춤화된 방식입니다 (자세한 내용은 Appendix A.7 참고). 문제를 이진 분류(binary classification) 작업으로 변환하여 실제 학습 데이터와 합성 샘플 간의 복잡한 관계를 식별하려는 시도입니다. 이진 분류 점수가 높을수록 해당 합성기가 멤버십 추론 공격에 취약하다는 것을 나타냅니다.
- 속성 노출 (Attribute Disclosure): 공격자가 이미 가지고 있는 일부 정보와 합성 데이터의 유사 레코드를 활용하여 레코드의 다른 추가적인 정보를 알아내려는 상황을 의미합니다. 공격자가 얼마나 정확하게 알 수 있는지를 분류 지표(classification metrics)로 정량화합니다. 속성 노출 지표가 높을수록 프라이버시 유출 위험이 높다는 것을 의미합니다. 공격자가 레코드의 일부 정보만 가지고 있다고 가정하므로, 프라이버시 측면에서는 멤버십 추론 공격보다 더 중요한 문제로 간주될 수 있습니다.
- Distance to Closest Record (DCR): 모든 실제 학습 샘플과 합성 샘플 간 L2 거리의 5번째 백분위수로 정의됩니다.
4.3 Results
Machine learning utility.
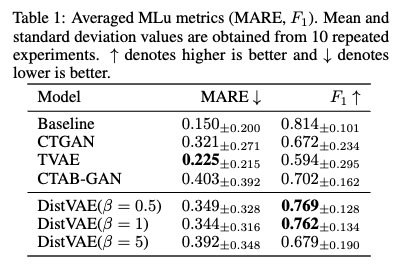
- MLu 정의: MLu는 생성된 합성 데이터를 사용하여 훈련된 머신러닝 모델의 예측 성능을 측정하는 지표입니다. 이상적인 고품질 합성 데이터 생성기는 실제 학습 데이터로 훈련된 모델과 유사한 예측 성능을 보여야 합니다. 이는 표 1에서 'Baseline' 성능과 비교하여 평가됩니다.
- DistVAE의 성능: 표 1의 결과에 따르면, DistVAE는 MARE (Mean Absolute Relative Error) 점수에서 경쟁 모델들과 유사하거나 우수한 성능을 보였으며, 특히 F1 score에서는 다른 비교 방법들(CTGAN, TVAE 63, CTAB-GAN)보다 우수한 성능을 달성했습니다. MARE: 회귀 작업에 사용되는 지표로, 값이 낮을수록 좋습니다. F1 score: 분류 작업에 사용되는 지표로, 값이 높을수록 좋습니다.
- β (beta) 값의 영향: MLu 성능은 β 값이 감소할수록 향상되는 경향을 보입니다. 이는 DistVAE가 생성하는 합성 데이터의 품질이 β 매개변수에 의해 조절될 수 있음을 시사합니다.
Statistical similarity.
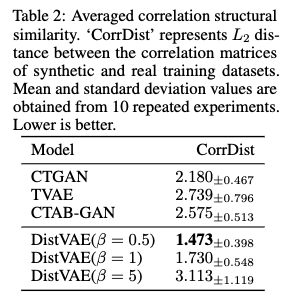
- 결합 분포 유사성 (Joint Distributional Similarity): 변수들이 함께 나타나는 방식, 특히 변수들 간의 상관 관계 구조를 얼마나 잘 포착하는지를 평가합니다.
- Table 2 결과: DistVAE는 CorrDist라는 지표에서 가장 낮은 점수를 기록했습니다. CorrDist (Correlation Distance): 합성 데이터의 상관 행렬과 원본 훈련 데이터의 상관 행렬 간의 L2 거리입니다. 상관 행렬은 데이터셋 내 모든 연속형 변수 쌍 간의 상관 계수를 보여줍니다. CorrDist 값이 낮을수록 변수들 간의 상관 관계 구조를 원본 데이터에 가깝게 보존했다는 의미입니다.
- DistVAE가 가장 낮은 CorrDist 점수를 얻었다는 것은 다른 비교 모델들 (CTGAN, TVAE, CTAB-GAN)에 비해 원본 데이터의 변수 간 상관 구조를 더 정확하게 유지했음을 의미합니다.
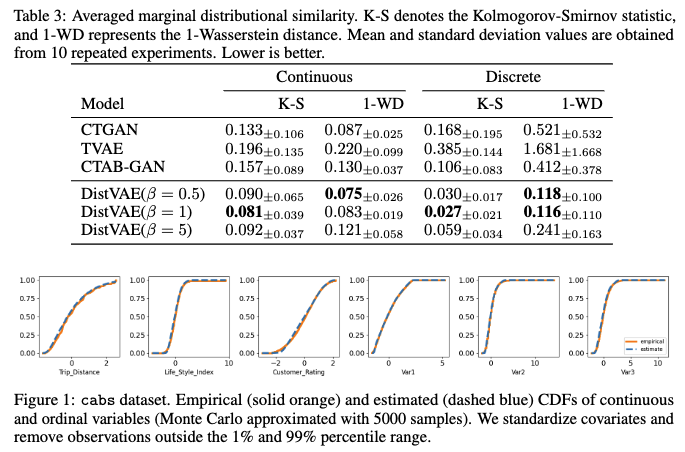
- 주변 분포 유사성 (Marginal Distributional Similarity): 각 변수의 개별 분포를 얼마나 잘 포착하는지를 측정합니다. 연속형 변수에는 Kolmogorov statistic과 1-Wasserstein distance를, 이산형 변수에도 유사한 지표를 사용했습니다. 이 지표들은 경험적 누적 분포 함수(empirical CDF) 간의 거리를 측정하며, 값이 낮을수록 주변 분포 유사성이 높음을 의미합니다.
- DistVAE 성능
DistVAE는 CorrDist 지표에서 가장 낮은 값을 기록하여, 다른 비교 모델들(CTGAN, TVAE, CTAB-GAN)에 비해 원본 데이터의 상관 구조를 가장 정확하게 보존함을 보여주었습니다 (Table 2 참조).
주변 분포 유사성에서도 DistVAE가 다른 모델들보다 뛰어난 성능을 보였습니다 (Table 3 참조). 이는 DistVAE가 관측된 데이터의 근본적인 분포를 성공적으로 포착하고 있음을 시사합니다. - β의 역할: VAE 프레임워크에서 KL-divergence 항의 가중치로 사용되는 파라미터 β는 합성 데이터의 품질에 영향을 미칩니다.
β 값을 낮추면 합성 데이터의 품질이 향상됩니다. 이는 상관 구조 유사성과 주변 분포 유사성 지표의 개선으로 확인됩니다.
이는 β가 데이터 품질과 개인 정보 보호 수준 간의 균형을 조절하는 역할을 한다는 것을 의미하며, 큰 β 값은 개인 정보 보호 수준은 높이지만 데이터 품질은 낮출 수 있습니다 (Section 4.3.2에서 더 자세히 다룹니다). - 시각적 확인: Figure 1은 cabs 데이터셋의 연속형 변수에 대해 원본 데이터의 경험적 CDF와 DistVAE로 추정된 CDF를 시각화하여 주변 분포 포착 성능을 보여줍니다. Appendix A.10에서는 더 자세한 통계적 유사성 점수와 다른 데이터셋의 CDF 시각화를 제공합니다.
Privacy preservability.
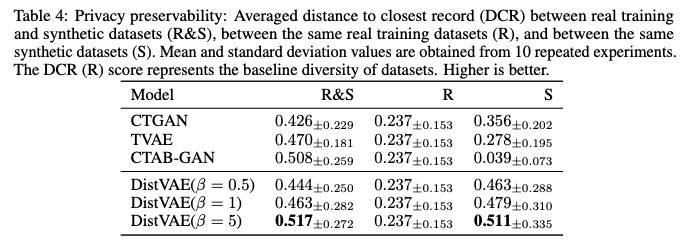
- DCR(Distance to Closest Record)
- DCR은 실제 데이터와 생성된 합성 데이터 간의 거리를 측정하여 개인정보 보호 수준을 평가하는 지표입니다.
- DCR 값이 높을수록 실제 데이터와 합성 데이터 간의 거리가 멀다는 뜻이며, 이는 실제 데이터의 정보가 합성 데이터에 노출될 위험이 낮다는 것을 의미합니다. 즉, 높은 DCR 값은 더 나은 개인정보 보호 성능을 나타냅니다.
- Table 4에는 세 가지 DCR 값이 제시
- R&S (Real & Synthetic): 실제 훈련 데이터셋의 각 레코드와 합성 데이터셋에서 가장 가까운 레코드 간의 L2 거리의 5번째 백분위수입니다. 실제 데이터가 합성 데이터로 인해 노출될 위험을 측정합니다.
- R (Real): 동일한 실제 훈련 데이터셋 내의 레코드 간 거리입니다. 이는 데이터셋 자체의 기본적인 다양성을 나타내는 기준선입니다.
- S (Synthetic): 동일한 합성 데이터셋 내의 레코드 간 거리입니다. 생성된 합성 데이터의 다양성, 즉 중복되지 않고 고유한 샘플을 얼마나 잘 생성하는지를 나타냅니다. S 값이 낮으면 중복된 레코드가 많다는 의미일 수 있습니다.
- DistVAE의 개인정보 보호 성능 (R&S DCR)
- Table 4에 따르면, DistVAE는 R&S DCR 값이 다른 비교 모델(CTGAN, TVAE, CTAB-GAN)보다 가장 높은 경향을 보입니다. 이는 DistVAE가 다른 모델들에 비해 개인정보 보호 성능이 우수하다는 것을 의미합니다.
- 특히, DistVAE 모델에서 β 값을 증가시킬수록 R&S DCR 값이 증가하는 것으로 나타났습니다 (β=0.5일 때 0.444, β=1일 때 0.463, β=5일 때 0.517).
- 이는 β 값을 조정함으로써 실제 데이터의 개인정보가 합성 데이터로 인해 노출될 위험 수준을 제어할 수 있음을 시사합니다. β 값이 높을수록 개인정보 보호 수준이 향상됩니다.
- DistVAE의 합성 데이터 다양성 (S DCR)
- DistVAE는 모든 β 값에서 합성 데이터셋 자체의 DCR (S) 값이 높게 나타납니다 (β=0.5일 때 0.463, β=1일 때 0.479, β=5일 때 0.511).
- 이는 DistVAE가 다양하고 중복이 적은 합성 샘플을 효과적으로 생성한다는 것을 보여줍니다.
- 반면, CTAB-GAN은 합성 데이터셋 (S)의 DCR 값이 0.039로 매우 낮습니다. 이는 CTAB-GAN이 합성 데이터셋 내에서 상당한 수의 중복 레코드를 생성했음을 나타냅니다.
- Attribute Disclosure
- Attribute disclosure(속성 노출)는 공격자가 특정 레코드에 대해 이미 알고 있는 일부 정보(공변량의 부분 집합)와 생성된 합성 데이터셋을 활용하여 해당 레코드의 알려지지 않은 다른 정보(추가적인 공변량)를 추론해내는 프라이버시 위험을 의미합니다.
- 이 연구에서는 F1 점수를 사용하여 이러한 속성 추론 공격의 성공 정도를 측정합니다. F1 점수가 낮을수록 공격자의 추론 성공률이 낮다는 의미이므로, 더 나은 프라이버시 보호 성능을 나타냅니다.
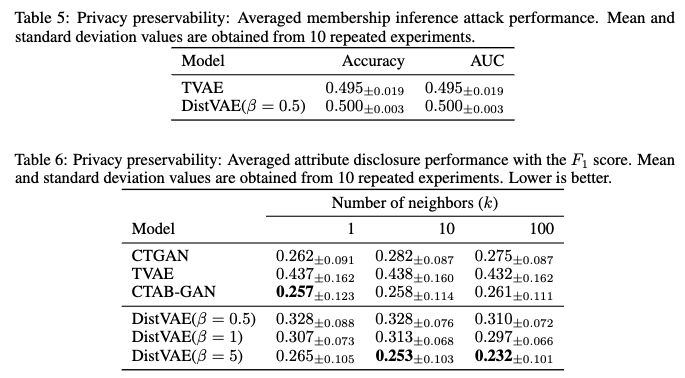
- Table 6 실험결과 해석
- Table 6은 CTGAN, TVAE, CTAB-GAN, DistVAE(β=0.5, 1, 5) 모델들의 평균 Attribute Disclosure F1 점수를 보여줍니다.
- 'Number of neighbors (k)'는 추론에 사용된 합성 데이터 내 유사 레코드의 개수를 의미합니다.
- DistVAE의 경우, β 값이 증가할수록 F1 점수가 감소하는 것을 확인할 수 있습니다 (예: k=10일 때 β=0.5에서 0.328, β=1에서 0.313, β=5에서 0.253).
- 이는 β 값이 커질수록 DistVAE가 생성한 합성 데이터의 프라이버시 보호 수준이 높아짐을 시사합니다.
다른 모델들과 비교했을 때, DistVAE(β=5)는 k=10 및 k=100인 경우 가장 낮은 F1 점수를 기록하며, Attribute Disclosure 측면에서 우수한 프라이버시 보호 성능을 보여줍니다
- 결론: Table 6의 결과는 DistVAE가 합성 데이터 생성 시 낮은 수준의 Attribute Disclosure 위험을 가지며, β 값을 조절함으로써 프라이버시 보호 수준을 제어할 수 있음을 나타냅니다.
Quantile estimation.

- Vrate: DistVAE 모델이 분위수 추정(Quantile Estimation) 성능을 얼마나 잘 수행하는지 평가하는 데 사용되는 지표입니다.
- 의미 해석
- Vrate 값이 alpha 에 가까울수록, 합성 데이터의 alpha 분위수가 실제 데이터의 alpha 분위수를 잘 추정하고 있음을 의미합니다. 이는 생성된 합성 데이터의 분포가 실제 데이터의 분포를 해당 분위수 수준에서 잘 반영하고 있다는 뜻입니다.
- 이상적으로는 Vrate 값이 alpha 와 같아야 합니다. 예를 들어, alpha=0.5 (중앙값)에서 Vrate(0.5)가 0.5 에 가깝다면, 합성 데이터의 중앙값이 실제 데이터의 중앙값을 잘 나타내고 있다고 볼 수 있습니다.
- 이 논문에서는 Vrate 와 alpha 의 차이인 |α − Vrate(α)| 를 사용하여 성능을 평가합니다. 이 값이 작을수록 분위수 추정 성능이 우수함을 나타냅니다.
- 논문의 평가 결과: 논문은 Vrate 평가 결과 |α − Vrate(α)| 값를 Table 7에 제시합니다. 표에 따르면, alpha 값이 증가할수록
|α − Vrate(α)| 값이 감소하는 경향을 보입니다. 이는 DistVAE가 낮은 분위수보다는 높은 분위수를 더 잘 추정함을 시사합니다. 특히 capital-gain 및 capital-loss와 같이 매우 비대칭적인(skewed) 연속 변수들 때문에 낮은 alpha 값에서의 분위수 추정이 불안정할 수 있다고 언급합니다.
5 Conclusion and Limitations
- 제안 방법의 목표 및 특징: DistVAE는 비모수적 접근 방식을 사용하여 관측 데이터의 근본적인 분포를 효과적으로 포착하는 것을 목표로 합니다. CRPS(Continuous Ranked Probability Score) 손실을 사용하여 CDF(Cumulative Distribution Function)를 직접 추정하며, VAE 프레임워크의 장점인 ELBO(Evidence Lower Bound) 유도를 유지합니다.
- 표 형식 데이터에서의 성능 확인: 제안된 디코더가 표 형식 데이터에 대한 생성 모델의 성능을 향상시킨다는 것을 확인했습니다.
- 한계점 -> 잠재 변수 주어졌을 때의 조건부 독립성 가정: 이러한 성능 향상은 잠재 변수가 주어졌을 때 관측 변수들이 조건부로 독립적이라는 가정에 의존합니다. 잠재 변수의 차원이 작을 경우 이 가정이 위반되기 쉬우며, 이는 디코더의 비모수적 적합이 근본적인 분포를 정확하게 나타내지 못하게 할 수 있습니다. 특히 인접 픽셀 값 간에 상당한 종속성이 있는 이미지 데이터의 경우, 저차원 잠재 공간에서 제안된 모델이 이미지 데이터 생성에 눈에 띄는 개선을 가져올지는 불확실합니다.
- 이미지 데이터 적용 가능성에 대한 논의
- 그럼에도 불구하고, CIFAR-10 과 같은 기존 이미지 데이터셋은 가우시안 분포에서 크게 벗어나는 픽셀 값 분포를 보이는 경우가 많습니다. 다른 이미지 데이터셋에서도 다봉성(multi-modality)이 관찰됩니다.
- 이러한 결과는 잠재 변수가 이미지 픽셀 간의 조건부 독립성을 효과적으로 포착할 수 있다면, 분포 학습 능력의 활용이 이미지 데이터의 근본적인 분포를 근사하는 데 유리할 수 있음을 시사합니다.
- 조건부 독립성 위반 및 주변부 분포 오지정(marginally misspecified distributions)으로 인해 발생하는 편향을 완화하는 것이 향후 연구에서 추가적인 결과 향상을 가져올 것으로 기대합니다.
- 향후 연구 방향
- Quantile 추정 성능 향상: 조건부 분위수 함수(conditional quantile functions)의 매개변수화를 더 유연한 단조 회귀 모델로 확장할 계획입니다.
낮은 분위수 수준을 더 잘 처리하기 위해 VAE 프레임워크에 UPR(Uniform Pessimistic Risk) [26]을 통합할 의향이 있습니다. - 시계열 분포 예측 모델로 확장: 조건부 VAE 프레임워크 [56]를 채택하여 DistVAE를 시계열 분포 예측 모델로 확장하는 것을 탐색하고 있습니다. 이를 통해 시계열 데이터에 방법론을 적용하고 분포 예측을 위한 새로운 길을 열 수 있을 것입니다.
- Quantile 추정 성능 향상: 조건부 분위수 함수(conditional quantile functions)의 매개변수화를 더 유연한 단조 회귀 모델로 확장할 계획입니다.
Reference
[1] Modeling Tabular data using Conditional GAN
[2] CTAB-GAN: Effective Table Data Synthesizing