Paper Review
[Paper Review] Gaussianization Flows (AISTATS 2020)
Seung-won Seo
2025. 6. 7. 05:17

Gaussianization Flows (AISTATS 2020)
Chenlin Meng* , Yang Song* , Jiaming Song, Stefano Ermon
Abstract
- 핵심 아이디어: Gaussianization Flow는 "Iterative Gaussianization"이라는 방법론에 기반하여 제안되었습니다. Iterative Gaussianization은 임의의 연속 확률 변수(continuous random vector)를 가우시안 분포(Gaussian distribution)로 변환시키는 반복적인 과정입니다. GF는 이 아이디어를 발전시켜 학습 가능한(trainable) 모델로 만들었습니다.
- 효율성
- 가능도(Likelihood) 계산: 데이터가 특정 모델에서 나올 확률을 계산하는 것이 효율적입니다. 이는 모델 학습 시 사용되는 최대 가능도(Maximum Likelihood) 방법을 효율적으로 수행할 수 있게 합니다.
- 샘플 생성(Sample Generation) / 역변환(Inversion): 학습된 모델로부터 새로운 데이터를 생성하는 과정, 즉 변환의 역과정이 효율적입니다. 이는 모델을 생성 모델로 활용하는 데 필수적인 요소입니다.
- 표현력(Expressivity): Gaussianization Flow는 특정 조건 하에서 연속 확률 분포에 대한 "Universal Approximators(만능 근사자)"임이 증명되었습니다. 이는 이론적으로 GF가 어떤 복잡한 연속 분포도 근사할 수 있음을 의미합니다.
- Multimodal Distributions 처리: 뛰어난 표현력 덕분에 GF는 여러 개의 봉우리가 있는 복잡한 분포(multimodal distributions)를 샘플 생성 효율성을 저하시키지 않으면서 잘 포착할 수 있습니다.
- 실험 결과: 다양한 표 형식 데이터(tabular datasets)에 대한 실험에서 Gaussianization Flow는 Real NVP, Glow, FFJORD와 같이 역변환이 효율적인 다른 정규화 흐름 모델들과 비교하여 더 좋거나 유사한 성능을 보였습니다.
- 실용적인 장점
- 쉬운 초기화: 모델 초기 설정이 비교적 용이합니다.
- 데이터 변환에 대한 강건성(Robustness): 훈련 데이터의 다양한 변환에 대해 더 안정적인 성능을 보여줍니다.
- 소규모 데이터에서의 일반화 성능: 훈련 데이터가 적을 때도 다른 모델들보다 더 나은 일반화 성능을 보였습니다.
1 INTRODUCTION
- Iterative Gaussianization: [1] 논문에서 처음 제안되었으며, 어떤 연속 확률 분포를 따르는 랜덤 벡터라도 표준 (다변량) 가우시안 분포로 변환할 수 있는 반복적인 절차이고, 핵심과정은 다음과 같다.
- Step-1 선형 매핑 (Linear Mapping): 데이터 포인트에 선형 변환(일반적으로 ICA 또는 PCA로 계산된 직교 행렬)을 적용합니다.
이 단계의 직관은 데이터 분포의 주변 분포(marginal distributions)에서 가장 "비(非)-가우시안적인" 방향을 찾는 것입니다. - Step-2 주변 분포 가우시안화 (Marginal Gaussianization): 선형 매핑된 데이터의 각 차원(feature)별 주변 분포를 개별적으로 가우시안 분포로 변환합니다. 이것은 각 주변 분포의 누적 분포 함수(CDF)를 추정하고, 이를 통해 각 차원을 균등 분포(uniform random variable)로 매핑한 다음, 표준 가우시안 분포의 역 CDF를 적용하여 가우시안 분포로 변환함으로써 달성됩니다. 이 단계를 통해 "비-가우시안성"이 감소합니다.
- 위의 두 단계를 충분히 여러 번 반복합니다.
- Step-1 선형 매핑 (Linear Mapping): 데이터 포인트에 선형 변환(일반적으로 ICA 또는 PCA로 계산된 직교 행렬)을 적용합니다.
- Iterative Gaussianization 의 중요한 두가지 한계점: 이 방법은 이론적으로 훌륭하지만 실제 적용에는 몇 가지 제약이 있습니다.
- 주변 분포 가우시안화의 어려움: 각 차원의 주변 분포를 가우시안 분포로 변환하는 것이 실제로는 어렵습니다. 특히 1차원의 경우에도 비모수적 방법(예: 커널 밀도 추정, Kernel Density Estimation, KDE)을 사용한 CDF 추정이 부정확하거나 튜닝하기 어려울 수 있습니다.
- 최적의 선형 매핑 탐색의 어려움: 주변 분포가 최대한 "비-가우시안적"이 되도록 하는 최적의 선형 매핑(회전)을 찾는 것이 어렵습니다. 전통적인 방법인 선형 ICA 등은 닫힌 형태의 해(closed-form solutions)가 없으며 대규모 데이터셋에서는 매우 느릴 수 있습니다.
- 목표: 본 논문은 이러한 Iterative Gaussianization 아이디어를 딥러닝 기반의 정규화 흐름 모델로 가져와 학습 가능하게 만들고, 기존 방법들의 실용적인 문제점을 해결하려고 시도합니다. 제안하는 방법론은 이론적 기반을 유지하면서도 실제 데이터에 더 잘 적용할 수 있는 새로운 방향을 제시합니다.
- Proposed methodology: Gaussianization Flows
- 기존 Iterative Gaussianization의 한계점 보완
- 기존 방법은 반복적인 절차를 따르지만, Gaussianization Flows는 이 절차를 파라미터화하여 전체 과정을 동시에 학습(jointly trainable)할 수 있도록 설계되었습니다.
- 이를 통해 실질적인 어려움이었던 주변 분포(marginal distributions)의 Gaussianization과 최적의 선형 변환(linear mapping)을 찾는 과정을 개선합니다.
- 파라미터화된 변환 모듈
- 선형 변환: 여러 개의 Householder transformations를 쌓아 학습 가능한 파라미터로 표현합니다. 이는 기존 방법에서 어려웠던 최적 회전 행렬(rotation matrix)을 찾는 과정을 대체합니다.
- 원소별 비선형 변환(Element-wise Non-linear Transformation): 학습 가능한 로지스틱 분포들의 혼합(trainable mixture of logistic distributions)의 누적 분포 함수(CDF)와 가우시안 분포의 역 CDF (\(\Phi^{-1}\))를 합성하여 표현합니다. 이는 각 차원의 주변 분포를 Gaussianization하는 과정을 파라미터화한 것입니다.
- Gaussianization 모듈 및 흐름 모델:
- 위의 선형 변환과 원소별 비선형 변환을 결합하여 미분 가능한 Gaussianization 모듈을 구성합니다. 이 모듈은 Jacobian 행렬식의 계산이 효율적이며 역변환(inversion)도 쉽습니다.
- 이러한 Gaussianization 모듈을 여러 개 쌓아 전체 Gaussianization Flows 모델을 만듭니다. 전체 모델 역시 쉽게 역변환할 수 있습니다.
- 보편 근사 능력 (Universal Approximators): 모델의 폭과 깊이가 충분하다면, Gaussianization Flows는 어떤 연속 확률 분포든 가우시안 분포로 변환할 수 있는 보편 근사자(universal approximator)임이 증명될 수 있습니다 (특정 정규 조건 하에). 이는 모델의 표현력이 이론적으로 보장됨을 의미합니다.
- 계층(Layer)의 해석 및 초기화
- Gaussianization Flows의 각 계층은 Iterative Gaussianization의 단계와 자연스럽게 연결됩니다. 예를 들어, 로지스틱 혼합 모델은 이전 계층의 선형 변환을 거친 데이터의 주변 분포를 학습하려 합니다.
- 학습을 개선하기 위해 로지스틱 혼합 모델의 파라미터를 Kernel Density Estimation (KDE)를 사용하여 데이터 기반으로 초기화할 수 있습니다. 이는 데이터의 재파라미터화(re-parameterizations)에 대한 견고성(robustness)을 제공합니다.
- 실험 결과
- Real NVP, Glow, FFJORD와 같은 다른 효율적인 가역 흐름 모델(efficiently invertible flow models)과 비교하여 여러 표 형식 데이터셋(tabular datasets)에서 더 좋거나 비등한 성능을 보여줍니다.
- 특히 적은 수의 훈련 데이터로 학습할 때 더 나은 성능을 보이며, 훈련 데이터의 다양한 변환에 대해 더 큰 견고성을 보여줍니다.
- 기존 Iterative Gaussianization의 한계점 보완
2 BACKGROUND
2.1 Density Estimation with Flow Models
- Density estimation 의 목표: 관측된 데이터셋(D)을 통해 알려지지 않은 연속적인 데이터 분포(pdata)를 확률 모델(pθ)로 근사하는 것입니다.
- Normalizing flow model: 이 모델은 데이터 x를 간단한 목표 분포(pz)를 따르는 잠재 변수 z로 변환하는 가역적이고 미분 가능한 변환 Tθ를 학습합니다.
- Change of variables formula: 데이터 x에서의 확률 밀도 pθ(x)는 잠재 변수 z에서의 확률 밀도 pz(z)와 변환 Tθ의 Jacobian 행렬식(determinant of the Jacobian matrix)을 사용하여 계산됩니다.
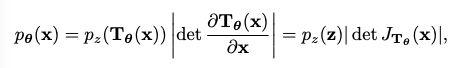
- Jacobian 행렬식의 중요성: 변수 변환 공식을 통해 효율적으로 확률 밀도 pθ(x)를 계산하고 최대 우도(maximum likelihood) 학습을 수행하기 위해서는 Tθ의 Jacobian 행렬식의 절댓값(|det JTθ(x)|)을 쉽게 계산할 수 있어야 합니다. 이러한 속성을 가진 모델을 정규화 흐름 모델이라고 합니다.
- 모델의 표현력 증가: 여러 개의 정규화 흐름 모델(T1, T2, ..., TL)을 순차적으로 연결(T = T1 ◦ T2 ◦ ... ◦ TL)하여 더 깊고 표현력이 풍부한 모델을 만들 수 있습니다. 각 구성 요소 모델 Ti가 가역적이고 Jacobian 행렬식이 계산하기 쉽다면, 결합된 모델 T 또한 동일한 속성을 유지합니다.
2.2 Iterative Gaussianization
- Normalizing flow model with maximum likelihood
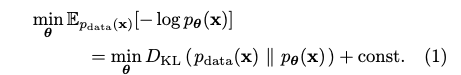
- KL Divergence의 Bijective Mapping 불변성 및 변환 (Eq. 2)
- Normalizing Flow 모델은 입력 x 를 잠재 변수 z 로 변환하는 Bijective Mapping (일대일 대응 함수) 입니다. KL Divergence는 이러한 Bijective Mapping에 대해 변하지 않는 성질이 있습니다.
- 이 성질을 이용하면, 실제 데이터 분포 p_{data}(x)와 모델 분포 p_{theta}(x) 사이의 KL Divergence를 최소화하는 문제가 Flow 모델을 통과한 데이터의 분포 p_{T_{theta}}(z))와 목표 분포인 표준 정규 분포 N(0, I) 사이의 KL Divergence를 최소화하는 문제와 동등함을 알 수 있습니다. 수식은 다음과 같습니다.
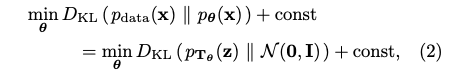
- 직관적 의미
- Maximum Likelihood 방식으로 Flow 모델을 학습시키는 것은 실제 데이터의 복잡한 분포를 가져와 Bijective Transformation T_{theta}를 적용했을 때, 그 결과 분포 p_{T_{theta}}(z) 가 우리가 미리 정해놓은 간단한 분포인 표준 정규 분포 N(0, I) 와 최대한 같아지도록 만드는 변환 T_{theta} 를 찾는 과정이라는 것입니다.
- 이러한 변환을 통해 임의의 연속 확률 벡터를 가우시안 형태로 바꾸는 작업을 Gaussianization이라고 합니다. 따라서 Flow 모델의 Maximum Likelihood 학습은 데이터를 Gaussianization하는 효율적인 Bijective Transformation을 학습하는 과정이라고 볼 수 있습니다.
- Rotation-Based Iterative Gaussianization (RBIG)
- 1차원 데이터 Gaussianization
1차원 데이터 x 를 가우시안 변수 z 로 변환하는 방법은 해당 데이터의 누적 분포 함수(CDF)인 F_{data}(x) 를 추정하고, 이를 표준 정규 분포의 역 CDF 에 적용하는 것입니다. 즉, 데이터 x 의 CDF 값을 구한 후, 그 값을 표준 정규 분포에서 찾을 수 있는 값으로 매핑하여 가우시안 변수를 얻습니다. - 고차원 데이터의 KL 발산 분해 (식(3))
- 데이터 분포 \(p(x)\)와 목표 분포인 다변수 표준 정규 분포 \(N(0, I)\) 간의 KL 발산입니다. 이 값이 0이 되면 데이터 분포가 목표 분포와 같아집니다.
- I(x) : Multi-information이라고 불리며, 데이터의 각 차원 구성 요소들 간의 통계적 의존성(상관 관계)을 측정합니다.
- Jm(x) : Marginal KL divergence의 합으로, 각 차원의 주변 분포(marginal distribution)가 1차원 표준 정규 분포와 얼마나 다른지를 측정한 값들의 합입니다.
- 1차원 데이터 Gaussianization

- Gaussianization의 목표
데이터 분포를 다변수 표준 정규 분포로 변환하기 위해서는 전체 KL 발산을 0으로 만들어야 합니다. 수식 (3)에 따라 이는 1. 각 차원이 독립과 2. Jm(x)=0 (각 주변 분포가 표준 정규 분포) 두 가지 조건을 동시에 만족해야 함을 의미합니다. - 반복적 Gaussianization (RBIG)
Gaussianization 및 Iterative gaussianization: from ica to random rotations에서 제안된 RBIG는 이 두 가지 목표를 달성하기 위해 1차원 Gaussianization과 회전 변환을 번갈아 적용하는 반복적인 접근 방식입니다.
과정:
현재 데이터의 각 차원에 대해 주변 분포를 추정합니다.
각 주변 분포에 1차원 Gaussianization을 적용하여 해당 차원을 표준 정규 분포에 가깝게 만듭니다.
변환된 데이터에 회전 행렬을 적용합니다.
이 과정을 데이터 분포가 다변수 표준 정규 분포에 수렴할 때까지 반복합니다. - RBIG의 원리
1차원 Gaussianization: 이 단계는 Jm(x) 값을 감소시킵니다. 중요한 점은 차원별로 독립적으로 적용되는 가역 변환(invertible transformation)이기 때문에 I(x) 값은 변하지 않습니다.
회전 변환: 회전은 데이터의 각 차원 간 통계적 의존성 구조를 변경합니다. KL 발산은 가역 변환에 불변이므로 전체 KL 발산 I(x) + Jm(x) 은 회전으로 인해 변하지 않습니다. 그러나 회전은 다음 1차원 Gaussianization 단계에서 Jm(x) 를 더 크게 감소시킬 수 있도록 데이터의 독립성 구조를 재배열하는 역할을 합니다. 이상적으로는 다음 1차원 Gaussianization 단계에서 Jm(x) 가 가능한 커지도록 하는 회전 행렬을 찾는 것이 좋습니다. 이를 통해 다음 단계에서 Jm(x) 를 0에 가깝게 만들 때 전체 KL 발산이 크게 감소하게 됩니다. 이러한 과정을 반복하면 매 단계마다 전체 KL 발산 값이 감소(또는 유지)되어 데이터 분포가 점차 다변수 표준 정규 분포에 수렴하게 됩니다. - RBIG의 실질적인 어려움
1차원 Gaussianization의 어려움: 실제 데이터에서 주변 분포를 정확하게 추정하고 1차원 Gaussianization을 수행하는 것이 어렵습니다. 특히 비모수적 방법인 커널 밀도 추정(KDE)은 정확도가 낮거나 튜닝하기 어려울 수 있습니다.
최적의 회전 행렬 찾기의 어려움: Jm(x) 를 최대화하는 최적의 회전 행렬을 찾는 것은 어렵습니다. ICA(Independent Component Analysis)와 같은 방법이 사용될 수 있지만, 이들은 폐쇄형 해(closed-form solution)가 없거나 대규모 데이터셋에서 계산 비용이 매우 높습니다. 랜덤 회전이나 PCA(Principal Component Analysis)를 사용하기도 하지만, 이 경우 수렴에 많은 반복이 필요할 수 있습니다.
3 METHOD
- Density estimation 을 위한 iterative Gaussianization 적용에서 직면하는 두가지 문제점
- 1차원 (1D) 가우시안화의 어려움: 특정 데이터 분포의 경우 각 차원별 분포를 1차원 가우시안 분포로 변환하는 것이 어렵습니다. 비모수적인 누적 분포 함수(CDF) 추정 방법(예: 커널 밀도 추정)은 정확도가 떨어지거나 튜닝하기 어려울 수 있습니다.
- 최적의 회전 행렬 탐색의 어려움: 데이터의 각 차원 간의 통계적 독립성을 최대화하는 최적의 회전 행렬을 찾는 것이 어렵습니다. 예를 들어 ICA(Independent Component Analysis) 기반의 회전 행렬은 폐쇄형 해(closed-form solution)가 없으며, 대규모 데이터셋에서는 계산 비용이 매우 높습니다.
- Gaussianization Flows (GF): 반복적 가우시안화 (RBIG)의 두 가지 핵심 구성 요소를 다음과 같이 개선합니다.
- 1D 가우시안화 대체: GF는 기존의 비모수적인 1D 가우시안화 단계를 학습 가능한 커널 레이어(trainable kernel layer)로 대체합니다. 이 레이어는 학습 가능한 파라미터를 가진 커널 밀도 추정 방식을 사용하여 1차원 분포를 더 효과적으로 가우시안화할 수 있도록 합니다.
- 고정 회전 행렬 대체: GF는 기존의 고정된 회전 행렬(예: PCA 또는 ICA로 계산된 행렬) 단계를 학습 가능한 직교 행렬 레이어(trainable orthogonal matrix layer)로 대체합니다. 이 레이어는 Householder 변환과 같은 기법을 활용하여 학습 과정을 통해 최적의 회전 변환을 찾도록 합니다.
- 문제 해결 방법: 학습 가능한 구성 요소를 도입함으로써 기존 반복적 가우시안화 방법의 실질적인 한계를 극복하고 밀도 추정 성능을 향상시킵니다.
3.1 Building Trainable Kernel Layers
- 기존의 Traditional non-parametric Kernel Density Estimation (KDE) 방식의 한계
- 높은 계산 복잡성: 각 샘플에 대한 KDE 계산은 샘플 수에 대해 제곱 복잡도를 가집니다. 이는 대규모 데이터셋에서 매우 비효율적입니다.
- 샘플 수 및 대역폭 선택에 대한 민감성: KDE 성능은 데이터 샘플 수에 크게 의존하며, 최적의 대역폭(bandwidth)을 설정하는 것이 어렵습니다.
- 제안하는 학습 가능한 커널 레이어
- 기존 KDE의 한계를 해결하기 위해, 각 데이터 차원에 대해 CDF를 직접 학습하는 방식을 제안합니다.
- 이는 '매개변수화된 KDE'와 유사한 형태로, 학습 가능한 앵커 포인트와 대역폭 매개변수를 사용합니다.
- d 번째 데이터 차원에 대한 학습 가능한 parameterize a CDF 는 식(6) 으로 정의됩니다.
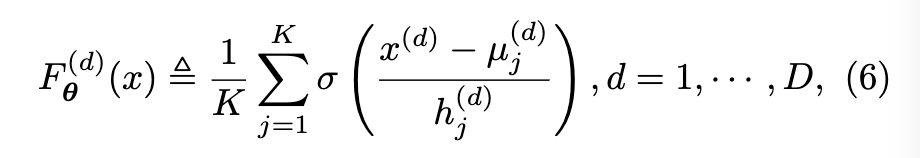
- d 번째 차원에 대한 가우시안화 변환은 다음의 식 (7) 과 같다.
- 식 (6) 의 학습가능한 CDF를 사용하여 d 번째 차원에 대한 가우시안화 변환을 식 (7) 과 같이 정의한다.
- 식 (7) 은 데이터의 d 번째 차원을 가우시안 분포를 따르도록 변환하는 학습 가능한 변환 함수입니다.
- 이 변환은 데이터의 순위(rank) 정보를 유지하면서 분포를 표준 정규 분포로 매핑합니다.
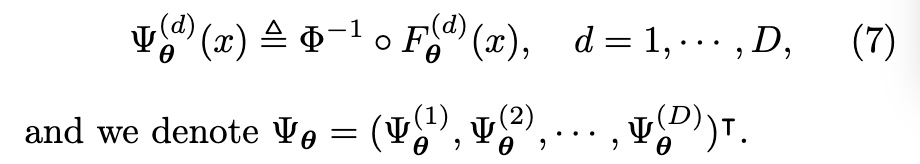
- 학습 가능한 커널 레이어 (Trainable Kernel Layers)
- 매개변수(앵커 포인트와 대역폭)를 학습함으로써 데이터에 더 잘 적응하고, 전통적인 KDE 방식보다 더 적은 샘플로도 좋은 성능을 얻을 수 있습니다. (논문에서는 20~100개의 앵커 포인트가 수천 개의 샘플을 사용하는 순수 KDE 방식보다 효율적이라고 언급).
- 식 (7) 의 각 차원별 변환의 집합이므로, 야코비안 행렬(Jacobian matrix)이 대각 행렬이 되어 행렬식 계산이 효율적입니다.
- 변환함수가 모두 단조함수 이므로 각 차원별로 이분법(bisection method) 등을 사용하여 효율적으로 역변환이 가능합니다.
- 학습 가능한 커널 레이어는 Gaussianization Flow 모델의 핵심 구성 요소가 되어, 데이터 분포를 효과적으로 가우시안 분포에 가깝게 변환하는 데 사용됩니다.
3.2 Building Trainable Rotation Matrix Layers
3.2.1 Householder Reflections
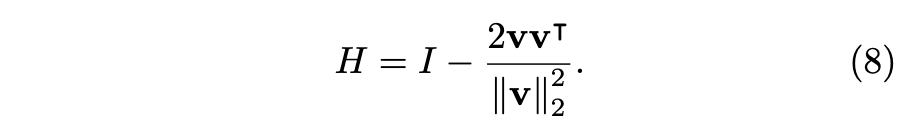
- Householder Reflections
- Householder Reflections 는 주어진 벡터 v에 의해 정의되는 대칭 행렬(symmetric matrix) H 입니다. (식(8))
- 이 행렬 H는 v에 수직인 초평면(hyperplane)에 대한 반사를 나타냅니다.
- Householder Reflections 행렬 H는 항상 직교 행렬(orthogonal matrix, HᵀH = I)이며 대칭 행렬(Hᵀ = H)입니다.
- Householder Reflections 를 이용한 rotation 행렬 표현
D x D 크기의 모든 직교 행렬 R은 최대 D개의 하우스홀더 반사 행렬의 곱으로 표현될 수 있습니다. (R = H₁H₂ ··· HD)
Gaussianization Flows에서는 여러 개의 학습 가능한(trainable) 하우스홀더 반사를 쌓아서 학습 가능한 직교 행렬 레이어를 구성합니다. - 효율적인 계산
역행렬 계산: 직교 행렬의 역행렬은 전치 행렬과 같습니다(R⁻¹ = Rᵀ). 따라서 하우스홀더 반사 행렬을 곱한 결과인 회전 행렬 R의 역행렬은 각 하우스홀더 반사 행렬의 전치를 역순으로 곱하여 효율적으로 얻을 수 있습니다. (R⁻¹ = (H₁···HD)⁻¹ = HD⁻¹···H₁⁻¹ = HDᵀ···H₁ᵀ = HD···H₁)
Jacobian 행렬의 행렬식 계산: 직교 변환의 Jacobian 행렬식의 절댓값은 항상 1입니다. 따라서 이 레이어의 Jacobian 행렬식 계산도 매우 효율적입니다. 여러 레이어를 쌓아도 전체 변환의 Jacobian 행렬식은 각 레이어 행렬식의 곱이므로 계산이 용이합니다. - 고차원 데이터 문제점 및 해결 방안
각 하우스홀더 반사는 D개의 모수(parameters, 벡터 v의 D개 성분)를 필요로 합니다. 따라서 D개의 하우스홀더 반사를 사용하여 직교 행렬을 완전히 모수화하려면 총 O(D²)개의 모수가 필요합니다.
데이터 차원 D가 작은 경우에는 문제가 없지만, CIFAR-10 (D=3072)이나 ImageNet (D ≈ 10⁶)과 같은 고차원 이미지 데이터의 경우 O(D²) 모수는 계산적으로 비현실적입니다.
이를 해결하기 위해, 논문에서는 모델 유연성과 계산 효율성 사이에서 절충하여 D보다 작은 수의 하우스홀더 반사를 사용하거나 이미지의 구조를 활용하는 패치 기반 모수화(patch-based parameterization) 방식을 제안합니다. 이 방식은 이미지를 작은 패치로 나누어 각 패치 내에서만 회전을 적용하여 모수의 수를 줄이는 방법입니다.
3.2.2 Patch-Based Rotation Matrices
- Patch-Based Rotation Matrices
- 이미지 데이터에 Gaussianization Flows를 적용할 때 사용되는 회전 행렬의 한 종류
- 도입 배경: 이미지의 픽셀은 멀리 떨어진 픽셀보다 주변 픽셀과 더 밀접하게 연관되어 있다는 직관에 기반합니다.
- 목표: Iterative Gaussianization(반복적 가우시안화) 방법론의 일종인 RBIG(Iterative gaussianization)에서 회전 행렬의 역할은 데이터의 각 차원(픽셀)을 최대한 독립적으로 만드는 것입니다. Patch-Based Rotation은 특히 의존성이 높은 부분(인접 픽셀)에 집중하여 독립성을 높이는 데 초점을 맞춥니다.
- 구조 및 매개변수화
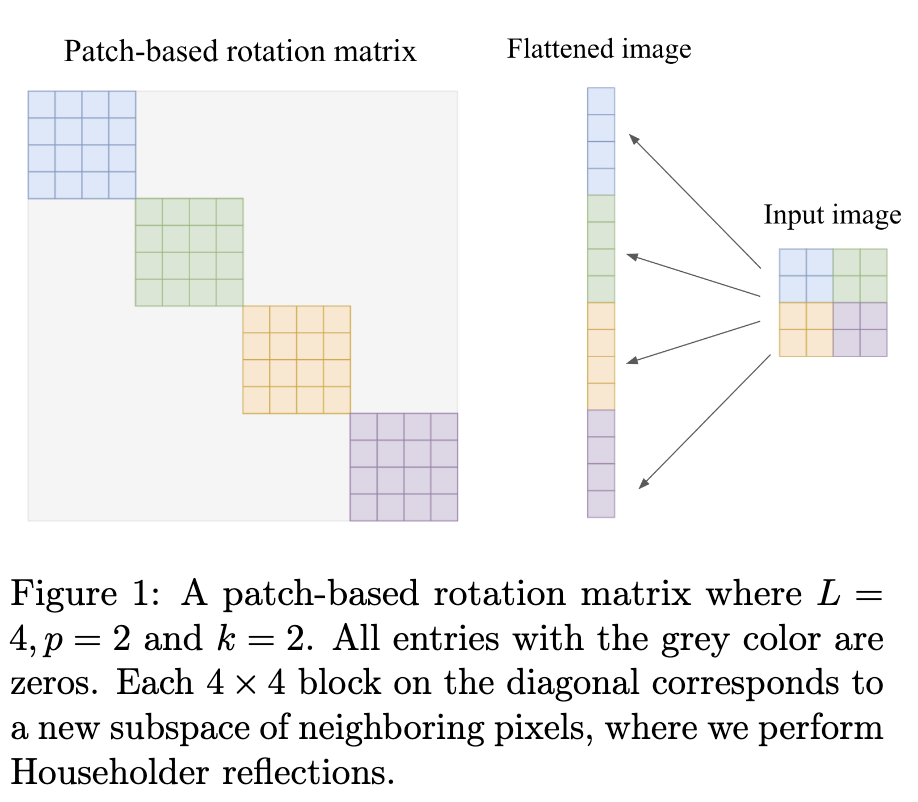
Patch-Based Rotation은 이 전체 행렬을 직접 매개변수화하는 대신, 작은 패치로 이미지를 분할합니다.
대각선 블록을 p^2 개의 Householder reflections로 매개변수화하여 Fig.1 과 같이 블록 대각선 회전 행렬을 만듭니다. 이는 필요한 매개변수 수를 크게 줄여줍니다. - 패치 간 의존성 도입: 회전은 각 \(p \times p\) 부분 공간 내에서만 이루어지므로, 서로 다른 회전 부분 공간(패치) 간의 의존성을 도입하기 위해 입력 벡터에 "shift" 연산을 적용합니다. 이 shift 연산은 픽셀 위치를 수평 또는 수직으로 순환적으로 이동시키는 방식입니다.
3.3 Deep Gaussianization Flows
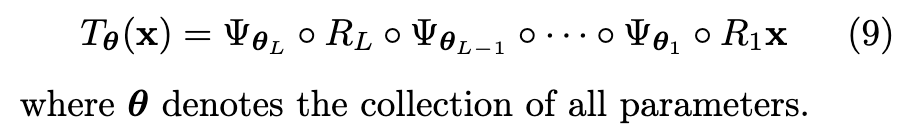
- Gaussianization Flows
- 식 (9) 와 같이 크게 두 가지 종류의 학습 가능한 레이어들을 번갈아 쌓아서 구성됩니다.
- 학습 가능한 커널 레이어 (Trainable Kernel Layers, Ψ): 이 레이어는 입력 데이터의 각 차원(dimension)별로 주변분포(marginal distribution)를 가우시안 분포처럼 변환하는 역할을 합니다.
- 직교 행렬 레이어 (Orthogonal Matrix Layers, R): 이 레이어는 입력 데이터에 회전 변환(rotation)을 적용합니다. 이 변환은 데이터의 차원들 간의 독립성을 높이는 데 도움을 줍니다. (계산효율성)
- 효율적인 순방향 및 역방향 계산: 데이터를 모델에 통과시키는 순방향 계산과 샘플 생성을 위한 역방향 계산 모두 효율적으로 수행할 수 있습니다.
- Jacobian 행렬식의 로그 값 계산 용이: 모델의 변환에 대한 Jacobian 행렬식의 로그 값을 닫힌 형태(closed-form)로 효율적으로 계산할 수 있습니다. 이는 최대 우도(maximum likelihood) 학습에 필수적입니다.
- 효율적인 샘플 생성: 역방향 계산이 효율적이므로 학습된 분포로부터 새로운 데이터를 효율적으로 생성할 수 있습니다.
- Maximum likelihood 학습 가능: Jacobian 행렬식 계산의 용이성 덕분에 모델 전체를 최대 우도 방식을 사용하여 한 번에 학습(jointly train)할 수 있습니다.
3.4 Gaussianization Flows are Universal Approximators
- Universal approximator 능력: 제안하는 flow-based model 인 GF는 컴팩트 서포트(compact support)를 가지는 모든 연속 분포를 표준 정규 분포(standard normal distribution)로 변환할 수 있음을 이론적으로 증명합니다. 이는 GF 모델이 복잡한 데이터 분포를 모델링할 수 있는 매우 강력한 표현 능력을 갖추고 있음을 의미합니다.
- 효율적인 역변환 가능한 Flow-based 모델 중 최초의 결과: 논문 저자들은 효율적으로 역변환 가능한(efficiently invertible) 정규화 Flow(normalizing flow) 모델 중에서 GF가 이러한 유니버설 근사자 능력을 갖추고 있음을 보인 첫 번째 연구 결과라고 강조합니다. 기존의 다른 효율적인 Flow 모델들은 이러한 이론적 보장이 부족했습니다.
- 기존 연구와의 연관성 및 차별점: 이 결과는 기존의 반복적 가우시안화(iterative Gaussianization) 방식, 특히 Gaussianization 논문(Chen and Gopinath, 2001)의 연구를 기반으로 합니다. 그러나 기존 연구는 주변 분포(marginal distribution)를 완벽하게 가우시안화할 수 있다고 이상적으로 가정한 반면, GF는 실제 학습 가능한 구성 요소인 '학습 가능한 커널 레이어(learnable kernel layers)'를 사용하여 주변 분포를 가우시안화한다는 점에서 차이가 있습니다.
- 유니버설 근사 능력 증명의 핵심 아이디어:
증명은 학습 가능한 커널 레이어의 핵심 구성 요소인 로지스틱 분포의 혼합 모델(mixtures of logistic distributions)이 단일 변수(univariate) 연속 밀도 함수(continuous densities)에 대한 유니버설 근사자임을 보여주는 것에서 시작합니다
이 사실을 바탕으로, 학습 가능한 커널 레이어가 충분히 많은 파라미터를 가질 때 임의로 우수한 주변 분포 가우시안화를 수행할 수 있음을 확인합니다. - 최종적으로, 충분히 많은 수의 주변 분포 가우시안화 레이어와 회전 행렬 레이어를 번갈아 쌓으면 (즉, 충분히 깊은 모델을 구성하면) Gaussianization Flow가 유니버설 근사자임을 아래의 Theorem 1 을 통해 증명합니다.

3.5 Building Invertible Networks with Proper Initializations
- Gaussianization Flow (GF)는 Iterative Gaussianization (RBIG)의 학습 가능한(trainable) 확장 버전입니다.
따라서 GF의 좋은 초기화는 RBIG를 활용하여 이루어집니다. - 학습 가능한 회전 행렬 레이어 초기화
각 Householder reflection 벡터는 isotropic Gaussian에서 샘플링하여 무작위로 초기화됩니다.
이는 RBIG에서 무작위 회전 행렬을 사용하는 것과 유사합니다.
계산 문제와 실제 결과의 유사성 때문에 ICA/PCA 레이어를 초기화에 사용하지 않습니다. - 학습 가능한 커널 레이어 초기화
데이터에 의존적인 초기화 방식을 사용합니다.
첫 번째 레이어의 KDE anchor point는 데이터셋에서 무작위로 N개의 샘플을 뽑아 초기화합니다.
일반적으로, 레이어 l+1의 KDE anchor point는 이전 레이어(l번째 학습 가능한 회전 행렬 레이어)의 출력을 사용하여 초기화합니다. - 초기화의 이점
GF 모델의 초기 상태는 반복적인 Gaussianization 방법(RBIG와 유사)에 해당하며, 이는 특정 수준까지 분포를 포착할 수 있습니다.
이 덕분에 GF는 초기 학습 단계에서 다른 Normalizing Flow 모델보다 뛰어난 성능을 보입니다.
좋은 초기화 덕분에 데이터의 re-parameterization에 대한 강건함(robustness)도 향상됩니다. - GF는 Iterative gaussianization: from ica to random rotations에서 제안된 RBIG 방법론을 기반으로 합니다. RBIG는 비학습 방식의 반복 절차였지만, GF는 이를 학습 가능한 모델로 만들면서 RBIG의 한계(예: 1D Gaussianization의 어려움, 최적 회전 행렬 찾기의 어려움)를 극복하고 효율적인 학습 및 샘플링을 가능하게 했습니다.
4 EXPERIMENTS
- Research Questions
- Is GF competitive against other methods in terms of density estimation (4.1, 4.2)?
- Does GF have better initialization than other normalizing flow models?
- Is GF robust against re-parameterization of the data with simple transformations (4.4)?
- Does GF achieve good performance when the training set is small (4.5)?
- Datasets
- synthetic 2D toy datasets
- benchmark tabular UCI datasets (Power, Gas, Hepmass, MiniBoone, BSDS300)
- Two image datasets: MNIST and Fashion-MNIST
- Baselines
- RealNVP
- Glow
- FFJORD
- MAF
- TAN
- NAF
- directly with RBIG
4.1 2D Toy Datasets
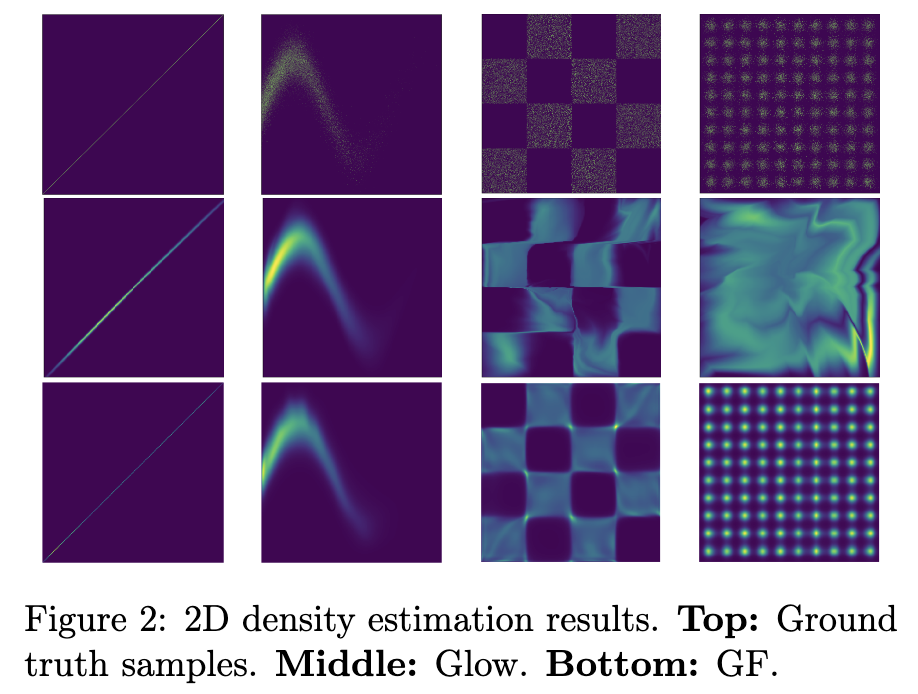
- 실험 결과
- Gaussianization Flows (GF): GF는 연속적이거나 불연속적인 분포, 그리고 연결되었거나 분리된(disconnected) 여러 모드 분포를 모두 잘 포착할 수 있음을 보여주었습니다.
- Glow: 반면에 Glow는 분리된 분포를 모델링하는 데 어려움을 겪는 모습을 보였습니다.
4.2 Tabular and Image Datasets
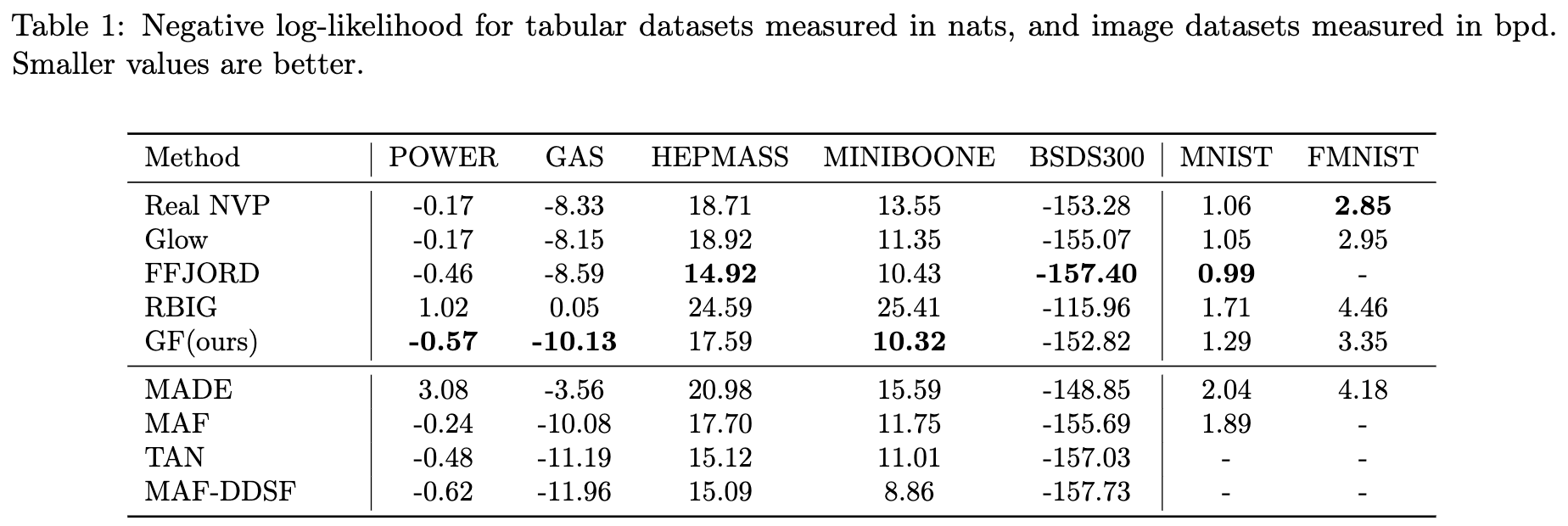
- 실험 결과 요약 (Table 1 참고)
- tabular 데이터셋에서 5개 중 3개 데이터셋에서 가장 좋은 NLL 값을 달성했으며, 나머지 2개에서도 비슷한 결과를 얻었습니다.
- RBIG보다는 모든 작업에서 훨씬 좋은 성능을 보였습니다.
- 이미지 데이터셋(MNIST, Fashion-MNIST)에서는 MAF, MADE와 같이 효율적으로 가역적이지 않은 모델을 포함한 다른 비(non-convolutional) 모델들보다 뛰어난 성능을 보였습니다.
4.3 Initial Performance
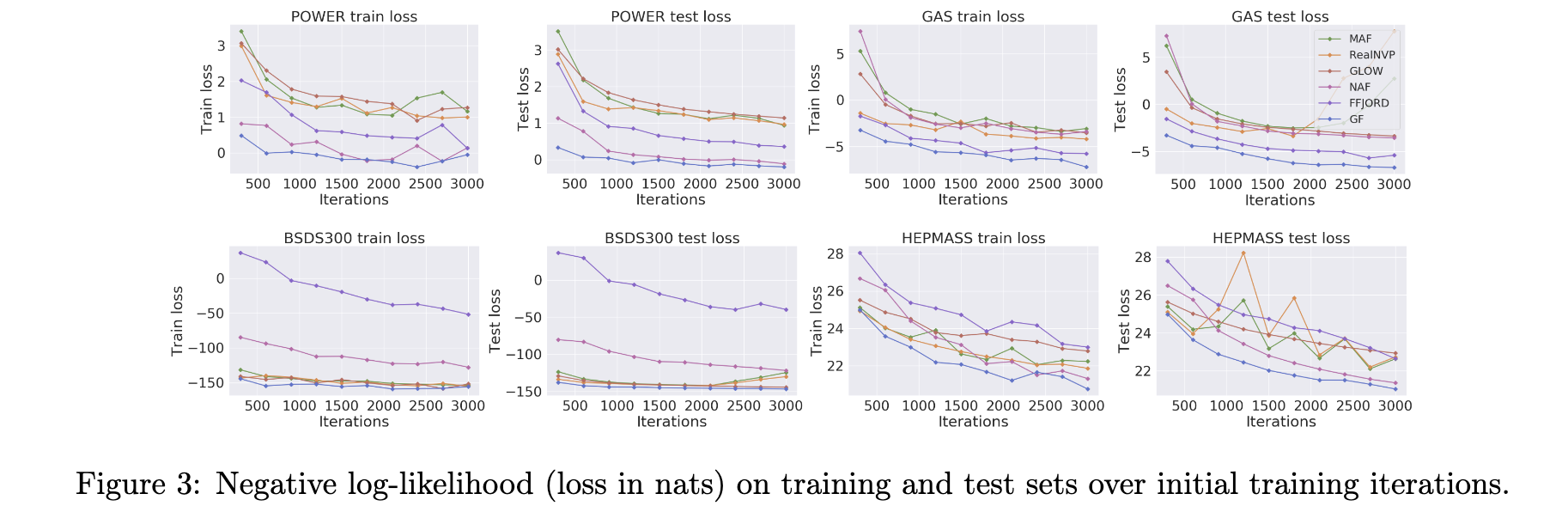
- Gaussianization Flow (GF) 모델의 데이터 의존적 초기화(data-dependent initialization) 방식 덕분에 훈련 과정이 다른 모델보다 더 빠르게 수렴(converge faster) 한다고 주장한다.
- 데이터 의존적 초기화
- GF는 Rotation-Based Iterative Gaussianization (RBIG)이라는 기존 방법론을 기반으로 구축되었습니다. GF는 RBIG의 초기 상태를 활용하여 모델을 초기화합니다.
- 학습 가능한 커널 레이어(trainable kernel layers)의 앵커 포인트(anchor points)와 대역폭(bandwidth)은 데이터셋의 랜덤 샘플을 사용하여 초기화됩니다 (섹션 3.5 참조).
- 이러한 데이터 기반 초기화는 모델이 훈련 시작부터 데이터 분포에 대한 어느 정도의 정보를 가지게 하여, 무작위 초기화 방식보다 유리하게 작용합니다.
- 빠르게 수렴
- 이는 훈련 초기 단계에서 모델의 성능이 다른 모델에 비해 빠르게 개선된다는 것을 의미합니다.
- 논문에서는 네 가지 테이블 형식 데이터셋(Power, Gas, Hepmass, MiniBoone)에 대한 실험 결과를 Figure 3에 제시하며 이를 뒷받침합니다.
- Figure 3의 실험결과는 훈련 초기 반복(iterations) 동안 GF가 RealNVP, Glow, FFJORD, MAF, NAF와 같은 다른 정규화 흐름(normalizing flow) 모델에 비해 전반적으로 더 나은 훈련 및 검증 성능(더 낮은 음의 로그 가능도, negative log-likelihood)을 달성함을 보여줍니다.
4.4 Stretched Tabular Datasets
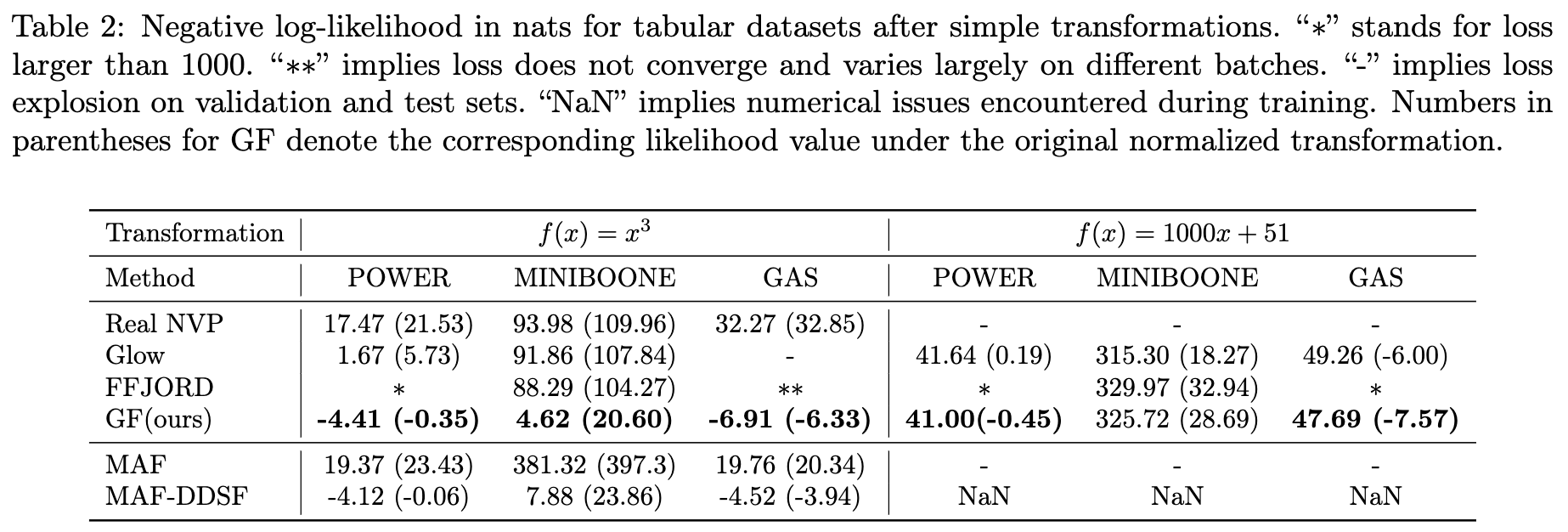
- Robustness 평가실험
- 문제 제기: 이상 탐지 같은 응용 분야에서는 데이터가 고정된 분포에서 오지 않거나 i.i.d.(독립항등분포)를 따르지 않는 경우가 많습니다. 이런 경우 데이터를 적절히 정규화하는 것이 어려워지므로, 모델 자체가 정규화되지 않은 분포에서도 잘 작동하는 강건성을 갖는 것이 중요합니다.
- Gaussianization Flows (GF): 두 가지 변환과 세 가지 데이터셋 모두에서 안정적이고 일관된 성능을 보였습니다. 괄호 안의 숫자는 변환된 데이터에서 계산한 가능도를 원래 정규화된 데이터 공간으로 되돌렸을 때의 가능도 값인데, GF는 변환 후에도 원래 데이터에서의 성능과 비교할 만한 가능도 값을 유지했습니다.
- 결론: 이러한 실험 결과는 Gaussianization Flows가 다른 효율적인 가역 흐름 모델(efficiently invertible flow models)에 비해 데이터의 분포 변화에 대해 더 나은 강건성을 가지고 있음을 시사합니다.
- 이전의 Normalizing Flow 모델들이 가역성이 효율적이지 않거나(MAF, NAF 등) 효율적이지만 표현력에 한계가 있을 수 있다는 문제(RealNVP, Glow)를 제기하고, Gaussianization Flows가 효율적인 가역성과 높은 표현력을 동시에 갖춘 모델임을 보입니다.
- 이 강건성 실험은 실제 데이터의 비정상성(non-stationarity)이나 분포 이동(distribution shift) 문제를 해결하려는 후속 연구(MAF-DDSF)에서도 중요하게 다루어지는 문제입니다. GF가 보여준 초기 수렴 속도와 강건성 특성은 이러한 실제 데이터 적용 문제를 해결하는 데 있어 중요한 진전으로 볼 수 있습니다.
4.5 Small Training Sets
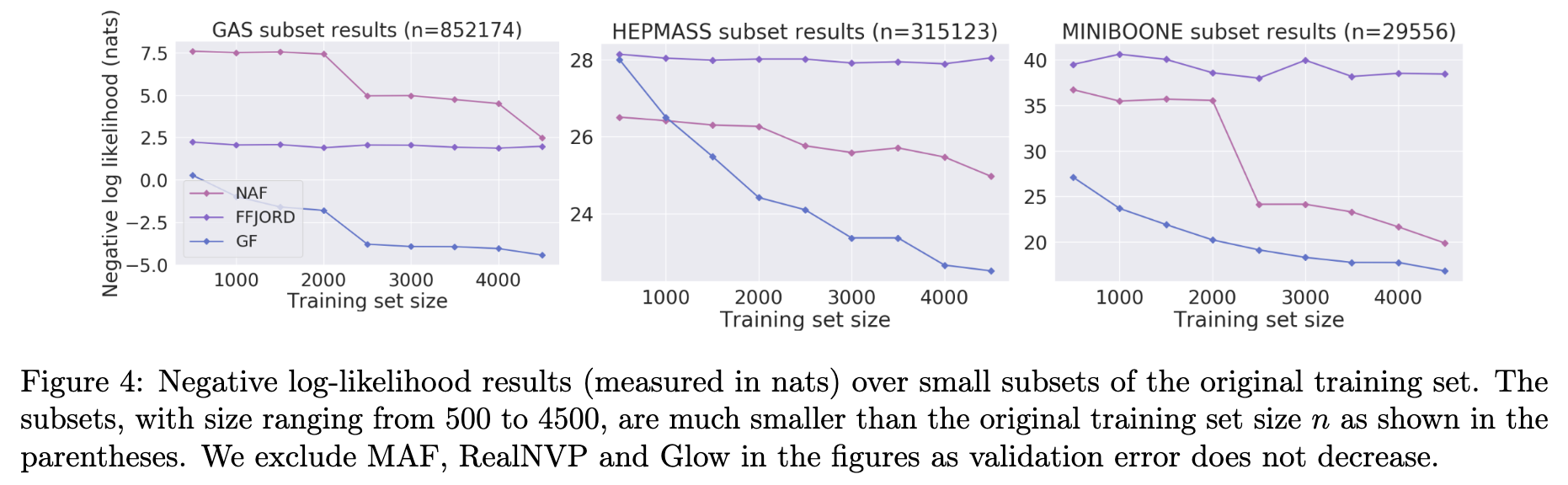
- 실험 목적: 연속적인 공변량 변화(continuous covariate shifts)가 있는 데이터 스트림과 같이 적은 샘플로 새로운 분포에 빠르게 적응하는 모델의 능력을 평가합니다. 이는 모델의 일반화 능력을 측정하는 데 중요합니다.
- 실험 설정
- 정규화된(normalized) 표 형식 데이터셋을 사용했습니다.
- 원본 학습, 검증, 테스트 데이터셋을 모두 섞은 후 무작위로 10,000개의 샘플을 선택하여 새로운 검증/테스트 세트로 사용했습니다.
- 학습은 원본 데이터셋보다 훨씬 작은 크기의 학습 서브셋을 사용하여 수행했습니다. 서브셋 크기는 500개부터 4500개까지 다양하게 설정했습니다.
- 실험 결과
- Figure 4는 다양한 크기의 학습 서브셋에 대한 모델별 Negative Log-Likelihood(nats 단위) 결과를 보여줍니다. (본 설명에서는 텍스트 내용에 기반하여 결과를 유추합니다.)
- MAF, Glow, RealNVP는 학습 데이터가 매우 적을 때 검증/테스트 세트에서 밀도 평가에 어려움을 겪는 것으로 나타났습니다. (학습 손실이 감소함에도 불구하고 검증/테스트 손실이 증가하는 현상 발생) 이로 인해 해당 모델들은 Figure 4 그래프에서 제외되었습니다.
- GF는 FFJORD 및 NAF 모델에 비해 모든 설정(다양한 서브셋 크기)에서 훨씬 뛰어난 성능을 보여주었습니다.
예외적으로 HEPMASS 데이터셋에서 서브셋 크기가 500일 때만 성능이 거의 비슷했습니다. - Findings: GF의 학습 가능한 KDE(Kernel Density Estimation) 레이어가 학습 데이터가 부족한 경우에도 테스트 세트에서 뛰어난 일반화 능력을 보여준다는 것을 시사합니다.
5 CONCLUSION
- Gaussianization Flows
- Rotation-based iterative Gaussianization (RBIG) 방법을 기반으로 하는 새로운 플로우 모델입니다.
- 데이터 분포를 가우시안 분포(Gaussian distribution)로 변환하는 것을 목표로 합니다.
- 학습 가능한 모델로 구현하여 RBIG의 단점을 개선했습니다.
- 주요 특징 및 장점
- 빠른 가능도(likelihood) 계산: 모델이 주어진 데이터를 얼마나 잘 설명하는지 나타내는 가능도를 효율적으로 계산할 수 있습니다.
- 빠른 샘플 생성: 모델로부터 새로운 데이터를 효율적으로 생성할 수 있습니다.
- Universal Approximator: 일부 정규 조건 하에 대부분의 연속 확률 분포를 근사할 수 있을 정도로 표현력이 뛰어납니다.
- 기존 모델 대비 성능
- Real NVP, Glow, FFJORD 등 기존의 효율적으로 역변환 가능한(efficiently invertible) 플로우 모델들과 비교했을 때, 동등하거나 더 나은 성능을 보입니다.
- 더 나은 초기화(initialization) 성능을 보입니다.
- 훈련 데이터의 분포 변화(distribution shifts)에 대해 더 강건(robust)합니다.
- 훈련 데이터의 양이 적을 때(small training sets) 더 뛰어난 일반화(generalization) 성능을 보여줍니다.
- Future work: GF의 장점과 다른 효율적으로 역변환 가능한 플로우 모델들의 장점을 결합하는 연구가 흥미로운 방향이 될 수 있습니다.
Reference
[1] Chen, S. S. and Gopinath, R. A. (2001). Gaussianization. In Advances in neural information processing systems , pages 423–429.