Paper Review
[Paper Review] Improving Neural Topic Models with Wasserstein Knowledge Distillation (ECIR 2023)
Seung-won Seo
2025. 6. 6. 20:51

Improving Neural Topic Models with Wasserstein Knowledge Distillation (ECIR 2023)
Suman Adhya and Debarshi Kumar Sanyal
Abstract
- 문제점: 신경망 토픽 모델 (NTMs) 은 상당한 메모리 공간(memory footprint)을 차지한다는 문제가 있습니다.
- Proposed methodology: 본논문에서는 이러한 문제를 해결하기 위해 지식 증류(knowledge distillation) 프레임워크를 제안합니다. 이는 토픽 품질의 손실 없이 컨텍스트화된 토픽 모델을 압축하는 것을 목표로 합니다.
- Knowledge distillation
- 제안하는 지식 증류 방법은 두 가지 목표를 최소화하는 데 초점을 맞춥니다.
- 소프트 레이블의 교차 엔트로피(cross-entropy of the soft labels): 성능이 좋은 큰 모델인 '선생님(teacher)' 모델과 압축하려는 작은 모델인 '학생(student)' 모델이 생성하는 소프트 레이블(soft labels) 간의 차이를 최소화합니다.
- 소프트 레이블은 모델 출력의 확률 분포를 의미하며, 선생님 모델의 분포를 학생 모델이 모방하도록 합니다.
- Wasserstein distance
- 잠재 분포(latent distributions) 간의 제곱 2-바서슈타인 거리(squared 2-Wasserstein distance): Teacher 모델과 student 모델이 학습한 문서의 잠재적인 토픽 표현(latent distributions) 간의 바서슈타인 거리를 최소화합니다.
- 바서슈타인 거리는 두 확률 분포 간의 '거리'를 측정하는 방법 중 하나로, KL 발산(Kullback-Leibler divergence)과는 달리 분포가 겹치지 않아도 의미 있는 거리를 계산할 수 있어 분포 간의 유사성을 측정하는 데 유용합니다. 논문에서는 특히 제곱 2-바서슈타인 거리를 사용합니다.
- 실험 결과
- 지식 증류로 학습된 학생 모델(distilled model)은 원래의 학생 모델보다 훨씬 높은 토픽 응집도(topic coherence)를 달성했습니다.
- 더 놀라운 점은 지식 증류로 학습된 학생 모델이 선생님 모델보다도 토픽 응집도가 더 높게 나왔다는 것입니다.
- 동시에 지식 증류로 학습된 학생 모델은 선생님 모델보다 훨씬 적은 수의 매개변수(parameters)를 가집니다.
- 제안하는 증류 모델은 다른 여러 경쟁적인 토픽 모델들보다도 뛰어난 토픽 응집도 성능을 보였습니다.
1 Introduction
- CombinedTM
- ProdLDA의 VAE에 사전 학습된 언어 모델(PLM, 예: Sentence-BERT)로 생성된 문서의 '문맥화된 표현
- (contextualized representation)'과 'Bag-of-Words (BoW)' 표현을 함께 입력으로 사용하는 문맥화된 토픽 모델입니다.
- 이를 통해 여러 벤치마크 데이터셋에서 최고 수준(state-of-the-art)의 토픽 일관성(topic coherence)을 달성했습니다.
- ZeroShotTM
- 문맥화된 토픽 모델의 한 종류입니다.
- 만약 PLM이 다국어(multilingual)를 지원하고, 인코더의 입력이 오직 PLM에서 나온 문맥화된 표현으로만 구성된다면, 한 언어로 모델을 학습시키고 다른 언어로 테스트할 수 있는 '제로샷(zero-shot)' 토픽 모델링이 가능해집니다.
- Network complexity 문제: VAE 네트워크의 복잡성을 높이면 토픽 일관성이 향상될 수 있지만, 이는 모델의 메모리 사용량(memory footprint)을 증가시켜 자원 제약이 있는 장치에서 사용하기 어렵게 만듭니다. 입력에 문맥화된 임베딩만 사용하는 것은 모델 크기를 줄일 수 있지만, 토픽 품질에 영향을 줄 수도 있습니다.
- Knowledge Distillation (KD)
- 더 크고 성능이 좋은 교사(Teacher) 모델의 지식을 더 작고 효율적인 학생(Student) 모델에게 이전하는 기법입니다.
- 하지만 이 논문은 비지도 학습 문제인 토픽 모델링에 KD를 적용합니다.
- 구체적으로 CombinedTM 교사 모델의 지식을 더 작은 ZeroShotTM 학생 모델로 이전합니다.
- 일반적인 KD와의 차이점
- 표준 KD 는 교사와 학생 모델이 생성하는 Soft Label 간의 Cross-Entropy를 최소화하고, 이들의 출력 분포 (latent distributions) 간의 Kullback-Leibler (KL) Divergence를 최소화하는 것을 목표로 합니다.
- 하지만 KL Divergence는 두 분포의 유사성이 매우 적을 때 값이 크게 커지고, 두 분포가 전혀 겹치지 않을 경우에는 무한대로 발산하는 문제가 있습니다.
- Wasserstein Distance 활용
- 이러한 KL Divergence의 문제를 피하기 위해, 이 논문에서는 증류 손실(Distillation Loss)에 2-Wasserstein Distance 를 사용합니다.
- Wasserstein Distance는 Optimal Transport 이론에서 비롯된 개념으로 두 분포가 얼마나 '가까운지'를 측정합니다.
- KL Divergence와 달리, Wasserstein Distance가 높다는 것은 두 분포가 실제로 매우 다르다는 것을 나타냅니다.
- Wasserstein Knowledge Distillation
- 교사와 학생 모델이 생성하는 Soft Label 간의 Cross-Entropy.
- 두 모델이 학습한 잠재 분포(Latent Distributions) 간의 제곱된 2-Wasserstein Distance
- Main contributions
- 신경망 토픽 모델을 위한 2-Wasserstein distance 기반 지식 증류 프레임워크를 제안했습니다 (Wasserstein knowledge distillation이라고 부름). 이는 VAE 간 지식 증류를 토픽 모델링에 적용한 첫 번째 연구입니다.
- 두 개의 공개 데이터셋에 대한 실험 결과, 증류된 모델은 학생 모델보다 훨씬 뛰어난 토픽 일관성을 보였고, 교사 모델보다도 더 나은 성능을 달성했습니다. 또한 다른 경쟁력 있는 토픽 모델들보다도 우수한 성능을 보여주었습니다.
2 Background on Wasserstein Distance
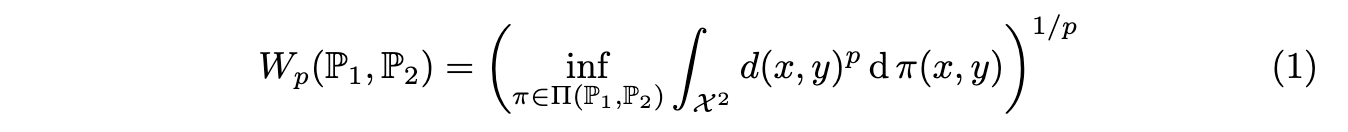
식 (1) 은 P1 분포를 P2 분포로 변환하는 데 필요한 최소 "비용"을 직관적으로 나타냅니다. d(x, y)는 한 지점에서 다른 지점으로 질량을 이동하는 데 드는 비용이며, π는 이러한 이동 계획입니다. Infimum은 가능한 모든 이동 계획 중에서 총비용이 가장 적은 계획을 찾는 것을 의미합니다.
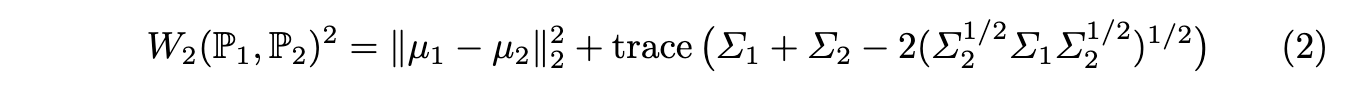
만약 공간 X가 Rn이고 거리 d가 유클리드 노름(Euclidean norm)이며, P1과 P2가 각각 평균 μ1, μ2 및 공분산 행렬 Σ1, Σ2를 가지는 정규 분포(normal distributions) N(μ1, Σ1) 및 N(μ2, Σ2)일 경우, 제곱 2-Wasserstein 거리는 식 (2) 와 같이 주어집니다.
- KL-divergence와의 비교
- Wasserstein 거리는 KL-divergence와 달리, 두 분포가 서로 겹치지 않아도 거리가 무한대가 되지 않으며, 분포 간의 실제 "거리"나 변환 "비용"을 더 직관적으로 나타냅니다.
- 본 논문에서는 이러한 특성 때문에 지식 증류 과정에서 KL-divergence 대신 Wasserstein 거리를 사용합니다.
- Teacher 모델과 학생 모델이 학습한 잠재 분포(latent distributions)가 가우시안 분포라고 가정하고, 두 모델의 잠재 분포 간의 제곱 2-Wasserstein 거리를 최소화함으로써 학생 모델이 선생님 모델의 지식을 효과적으로 전달받도록 합니다.
3 Proposed Framework for Knowledge Distillation
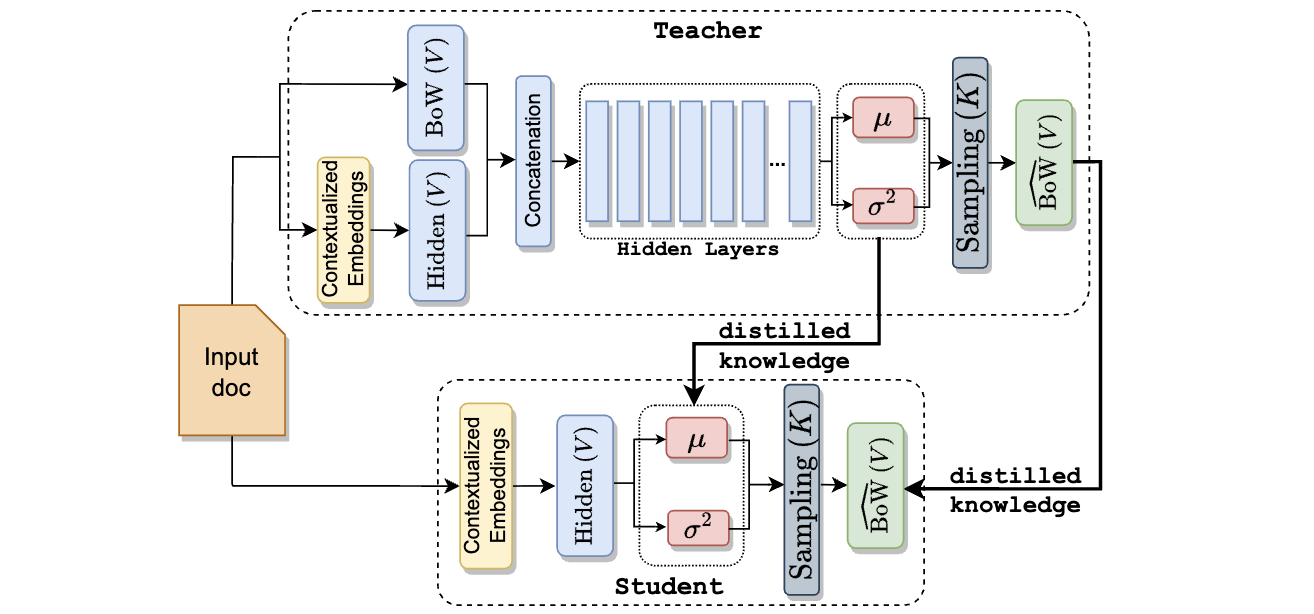
Proposed Framework
- Teacher 모델 (T): CombinedTM
입력으로 문서의 BoW(Bag-of-Words) 표현과 문맥화된 임베딩을 연결한 값을 사용합니다.
인코더는 여러 개의 히든 레이어를 가진 피드-포워드 신경망(FFNN)입니다. - Student 모델 (S): ZeroShotTM
입력으로 문서의 문맥화된 임베딩만을 사용합니다.
인코더는 하나의 히든 레이어를 가진 FFNN입니다 (Teacher보다 작음).
학습 시에는 BoW 벡터가 필요하지만, 학습된 인코더만 사용하여 토픽을 추론할 때는 필요하지 않습니다. - KD 를 사용한 Student 모델 학습
- 식 (3) 의 objective function 을 통하여, Teacher 모델을 먼저 학습시키고 Student 모델 학습시에 Teacher 모델의 가중치는 frozen 합니다.
- Student 모델의 손실함수는 VAE loss, KD loss 두가지로 구성됩니다.
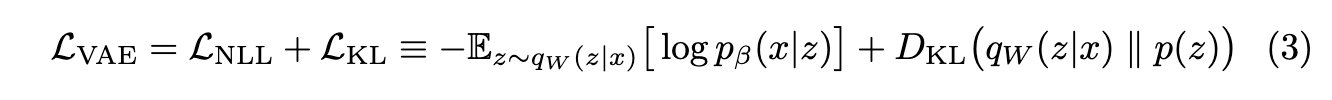
- KD loss
- KD loss 는 student model 의 encoder 와 decoder 를 위한 두개의 손실함수로 구성됩니다. 첫번째는 Wasserstein distance 기반의 loss, 두번째는 cross-entropy 기반의 loss 입니다.
- Teacher model 의 인코더가 가진 지식을 증류하기 위해, 두 모델의 각 인코더의 output 인 latent distribution 간의 Wasserstein distance 를 활용한 loss 를 식 (4) 와 같이 계산합니다.
- 두 모델의 각 디코더의 output (즉, logit) 인 재구성된 문서의 단어분포간의 cross-entropy 를 활용한 loss 를 계산하여, 최종적인 KD loss 를 식 (5) 와 같이 계산합니다.
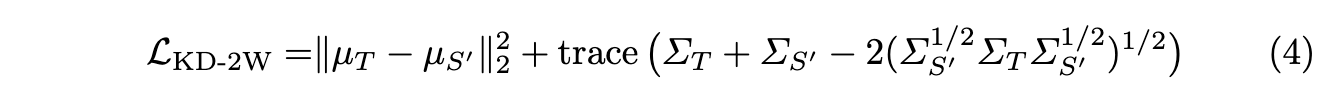
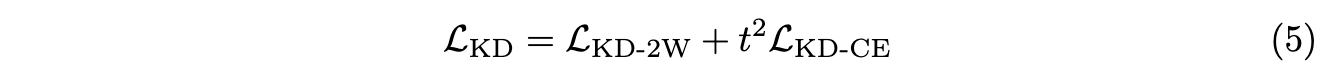
- Overall training objective: Student model 학습을 위한 최종적인 loss function 은 식 (6) 과 같습니다. alpha 값은 0 과 1 사이의 hyperparameter 입니다.
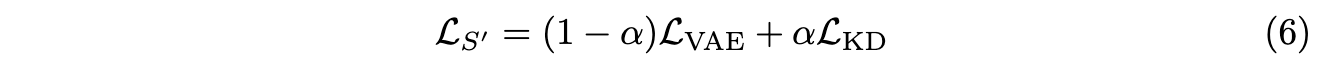
4 Experimental Setup
- Datasets: 20NG, M10
- Evaluation metrics: Normalized Point-wise Mutual Information (NPMI), Coherence Value (CV)
- 컨텍스트 임베딩 (input documents)
- Teacher 모델의 인코더는 paraphrase-distilroberta-base-v2 에서 얻은 768차원의 SBERT 임베딩을 사용했습니다.
- Student (S 및 SKD) 모델의 인코더는 all-MiniLM-L6-v2 에서 얻은 384차원의 SBERT 임베딩을 사용했습니다. 이는 Teacher 모델보다 작은 모델입니다.
- Baselines
- ProdLDA
- NeuralLDA
- ETM
- LDA
- ZeroshotTM (i.e., Teacher model)
- CombinedTM (i.e., Student model)
5 Results
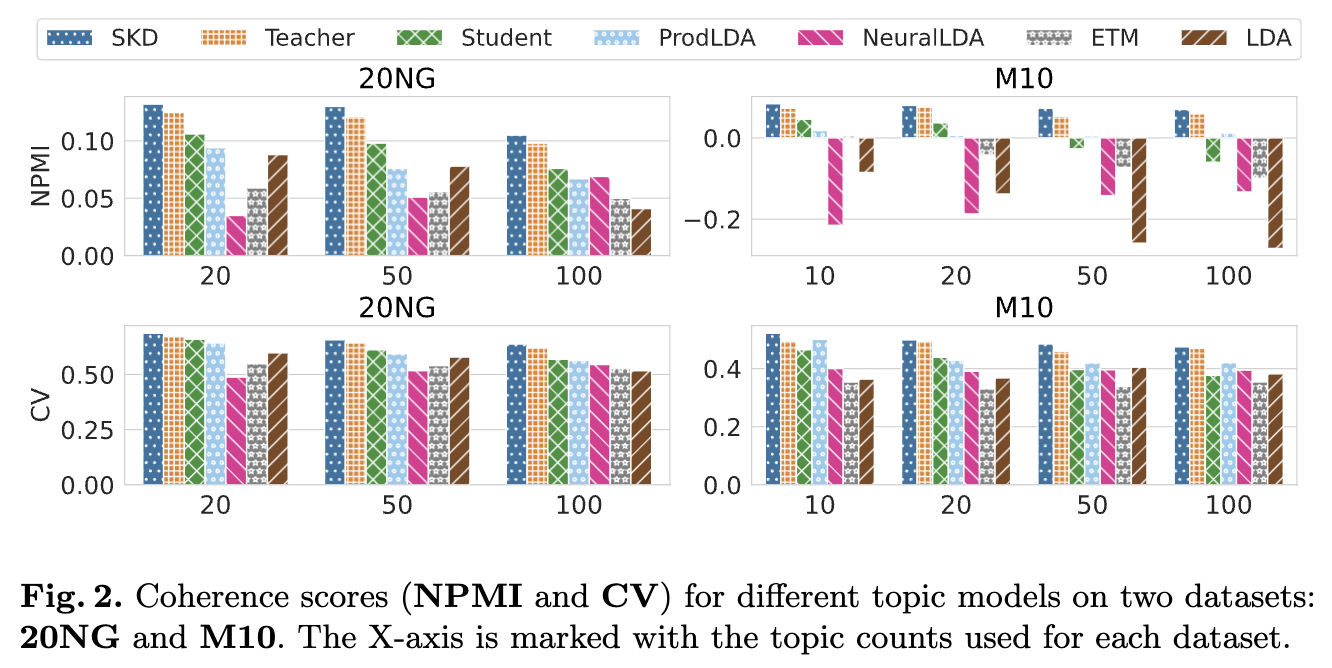
본 논문에서 보여준 실험결과는 제안된 Wasserstein knowledge distillation 기법을 통해 학습된 학생 모델(SKD)이 원래의 학생 모델(ZeroshotTM 즉, S) 과 심지어 더 큰 교사 모델(CombinedTM 즉, T)에 비해 모델 크기와 토픽 품질 측면에서 어떤 성능을 보이는지 설명합니다.
- 모델 크기 비교
- 학생 모델(S)과 지식 증류된 학생 모델(SKD)은 교사 모델(T)보다 파라미터 수가 적어 모델 크기가 더 작습니다.
- 모델 크기는 SBERT 임베딩 차원, 은닉층의 개수와 크기, 토픽 수, 어휘 크기 등 다양한 요인에 따라 달라집니다.
- 예를 들어, 20NG 데이터셋의 20개 토픽의 경우, T 모델은 6.14MB이지만 SKD 모델은 2.74MB로 55.4%의 크기 감소를 보였습니다. 전반적으로 37.6%에서 56.3% 범위의 모델 압축률을 달성했습니다.
- Topic quality (NPMI 및 CV)
- SKD 모델은 모든 토픽 설정과 데이터셋(20NG, M10)에서 가장 높은 NPMI 및 CV 점수를 기록했습니다.
- T, S, SKD 모델 중에서 SKD가 S보다 훨씬 우수하고, T보다도 약간 더 좋은 성능을 보였습니다.
- 20NG 데이터셋에서 SKD는 S 대비 NPMI 점수가 최대 38.2% 향상되었고, T 대비 최대 7.4% 향상되었습니다.
- M10 데이터셋에서는 K=50, 100일 때 SKD가 S 대비 NPMI 점수가 100% 이상 향상되었고, T 대비 최대 37.7% 향상되었습니다.
- 작은 학생 모델이 교사 모델보다 우수한 성능을 보이는 것은 놀라운 결과이지만, 다른논문의 연구결과에 따르면 supervised learning task 에서도 이전에 보고된 바 있습니다
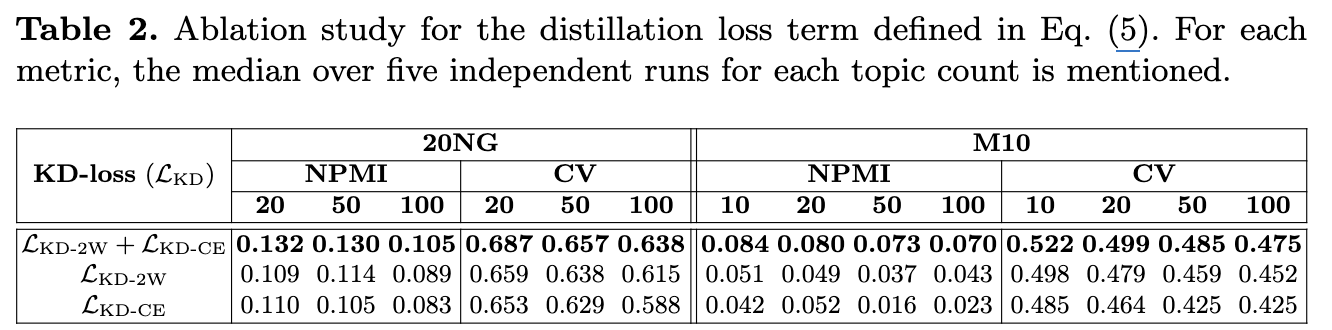
- Ablation Study: 지식 증류 손실 함수의 중요성
- 지식 증류 손실 LKD (식 (5))에서 두 가지 손실 항, 즉 2-Wasserstein 거리 손실 (LKD-2W)과 교차 엔트로피 손실 (LKD-CE) 중 하나라도 제거하면 SKD의 NPMI 및 CV 점수가 하락했습니다 (표 2 참고).
- 이는 더 간단한 모델과 성능이 낮은 SBERT를 사용하는 학생 모델(S)의 성능이 낮더라도, 교사의 인코더와 디코더로부터 증류된 지식이 학생 모델의 성능을 크게 향상시킨다는 것을 보여줍니다. 두 손실 항 모두 증류 과정에 필수적입니다.

- Qualitative Analysis
- 20NG 코퍼스에서 T, S, SKD가 학습한 일부 토픽을 비교한 결과 (표 3), SKD가 T의 토픽과 더 많은 단어 중복을 보여 S보다 T와 더 유사한 토픽-단어 분포를 학습했음을 알 수 있었습니다.
- 흥미롭게도, SKD의 네 번째 토픽은 T의 네 번째 토픽(주로 헬스케어 관련)보다 헬스케어 관련 단어를 더 많이 포함하여, SKD가 T보다 더 일관성 있는 토픽을 생성할 수 있음을 시사합니다.
6 Conclusion
- 제안된 방법: Contextualized Topic Model을 압축하기 위해 2-Wasserstein 손실을 활용한 지식 증류 프레임워크를 사용했습니다.
- KD 는 크고 성능 좋은 Teacher 모델의 지식을 작고 효율적인 Student 모델에게 이전하는 기술입니다.
- 실험 결과와 성능개선
- 두 가지 공개 데이터셋(20NG, M10)에 대한 실험을 통해 제안된 방법(Wasserstein Knowledge Distillation로 훈련된 Student 모델, SKD)의 효과를 입증했습니다.
- 성능 개선: 압축된 Student 모델(SKD)은 원래의 Student 모델보다 훨씬 높은 토픽 일관성(Topic Coherence)을 달성했으며, 심지어 Teacher 모델의 성능까지 능가하는 결과를 보여주었습니다. 이는 모델 크기를 크게 줄이면서도 성능 저하 없이, 오히려 성능 향상까지 이루어냈음을 의미합니다.
- 새로운 접근 방식: 저자들은 이 방법이 신경망 토픽 모델에 대한 새로운 지식 증류 방법이라고 언급하고 있습니다.
- Future work: 이 방법을 분석적으로 더 깊이 연구하고, 다른 신경망 토픽 모델에도 적용하여 지식을 증류하는 방법을 모색할 계획이라고 밝히고 있습니다.