Graph Representation Learning - (2) Node Embedding & Basic GNN
Node Embedding
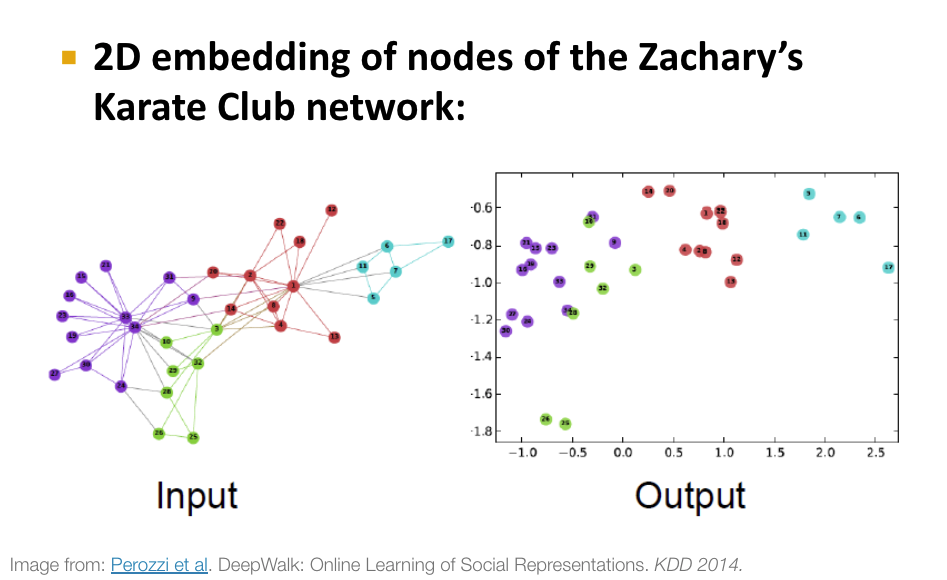
그래프 데이터에서 node 를 임베딩하는 방법에는 다양하게 있습니다.
노드 임베딩이란 , 그래프는 일반적으로 non-euclidean space 에 존재하는데 이를 그래프안에 있는 각 노드들을 euclidean space (저차원공간) 에 임베딩해주는것 입니다. 그러면 노드임베딩의 목표는 , 유사한 노드는 embedding space 에서 근처에 위치하게 임베딩해주는 것 입니다.
Node Embedding 에는 크게 두가지 방법이 있습니다.
- Shallow embedding method : Node2Vec , DeepWalk , LINE , ...
- Neural net-based method
Shallow Embedding Method
Shallow embedding method 에서는 노드임베딩을 위해 다음과 같은 두 노드의 similarity 를 고려합니다.
- 두 노드의 연결성
- 두 노드의 이웃 공유 여부
- 두 노드의 구조적 역할
- dot product
그러면 Shallow Embedding method 에서는 Node Similarity 를 학습하기 위해 어떻게 최적화를 할까요?
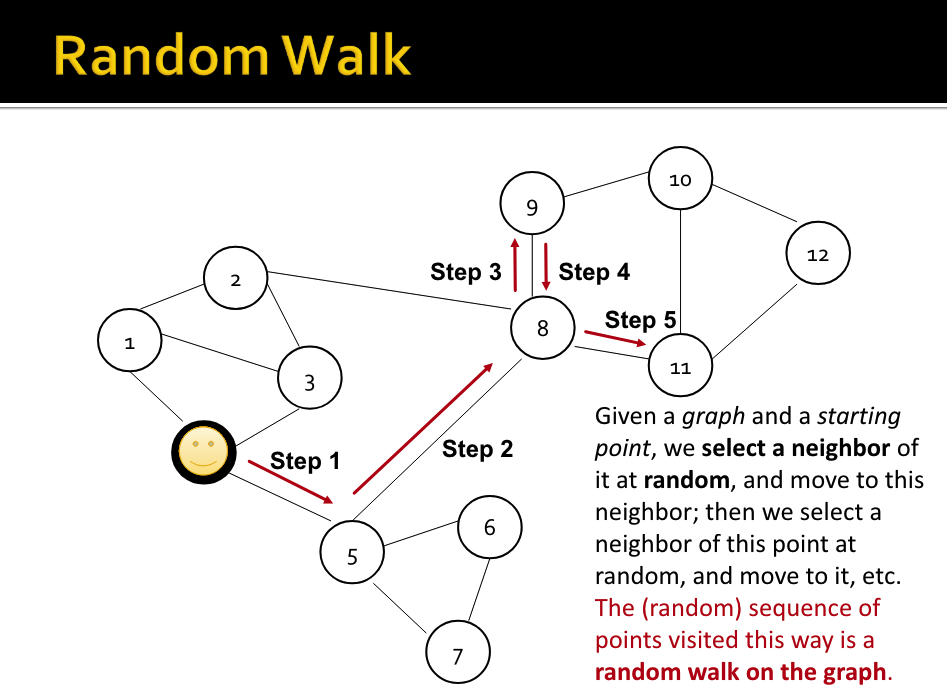
그 방법을 바로 Random Walks 라고 합니다.
Random Walk 알고리즘이란 , 바로 노드 위를 랜덤하게 선택해서 이동하는 것 입니다.
랜덤하게 neighborhood 를 선택해서 거쳐가는 point sequence 로 이용합니다.
(여기서는 Shallow embedding 은 상세히 설명하진 않겠습니다.)
Neural Message Passing : Neural net-based Node Embedding
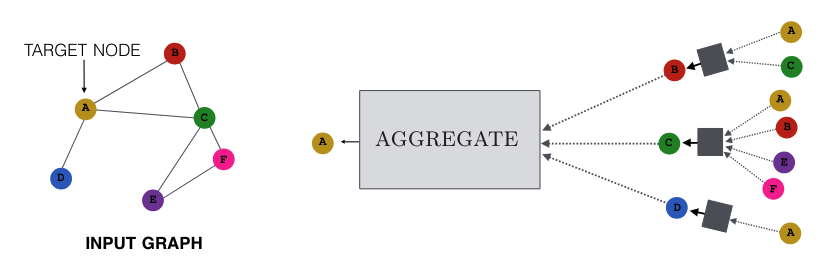

GNN 의 기본원리 : Input 그래프 내에서 인접한 노드들을 기반으로 Node Embedding 을 합니다.
이웃한 노드(neighborhood) 들의 노드 정보를 하나로 합치고 이를 matrix 와 곱한 후 Non-linear function 을 통과시킵니다.
그리고 이 과정을 Aggregation 이라고 합니다. 마치 일반적인 Neural net 에서 하나의 hidden layer 를 거치는것과 유사합니다.
이 Aggregation 하는 방법의 차이에 따라 GCN , GAT 등으로 달라집니다.
Aggregation 은 GNN 에서 가장 핵심원리이기에 매우 중요합니다.
Aggregation 과정을 더 자세하게 수학적으로 알아보면 다음과 같습니다.
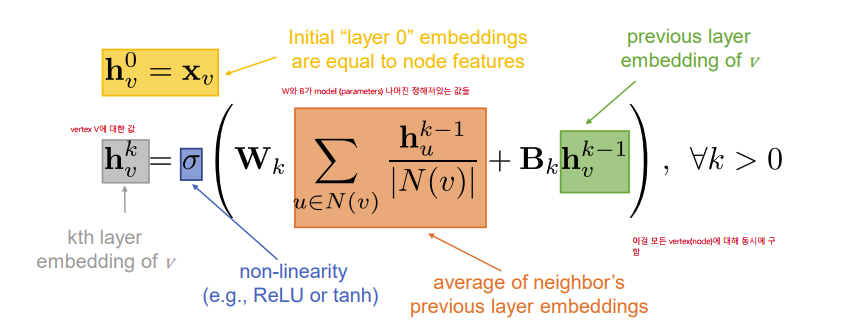
The Simplest GNN
